Coursera Machine Learning
Week3【学習メモ】【機械学習】

スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。

機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース（1日1~2時間ペース？）としていますが、気にせずに理解できているか確認しながら進めていこうと思います。

Ⅰ．Logistic Regression

分類問題に線形回帰を適用するのはあまりいいアイデアではないため使用しない。

分類問題に線形回帰を使用するとyの値が0か1に等しくなる場合でも、仮説が1以上であったり、0以下の出力をするなど奇妙なことが起きる。

そのため、ロジスティック回帰と呼ばれるものを使用します。ロジスティック回帰の予測では常に0から1の間であり、それ以上でもそれ以下にもなりません(つまり、上記のようにはならない)。

ロジスティック回帰は「回帰」がついているが、実際には分類アルゴリズムです(分類の手法のため注意)。ラベルyが0または1の場合に離散値である設定に適用する分類アルゴリズムです。

分類問題は回帰問題と同じですが、予測したい値が少数の離散値のみをとる点が異なります。

Hypothesis Representation

シグモイド関数(ロジスティック関数)が登場します。
前回の講義で学習した仮説にシグモイド関数を合わせると下記の式になります。

\(h_\theta(x)= g(\theta^T x)\)
\(z = \theta^T x\)
\(g(z) = \frac{1}{1+e^{-z}}\)
\(h_\theta(x)=\frac{1}{1+e^{-\theta^T x}}\)

シグモイド関数はz軸(横軸)がマイナスの無限大になると0に近づき、プラスの無限大になると1に近づく。つまり、シグモイド関数は0から1の間の値を提供する。
そのため、仮説として取り得る値の範囲は\(0\leq h_\theta(x)\leq 1\)のようになる。

\(h_\theta(x)\)は確率を表しており、\(h_\theta(x)=0.7\)なら1の確率が70%と言う意味になる。
数式で表すと\(h_\theta(x)= P(y=1|x;_\theta)\)という形になり、これはある\(x\)のときに\(y=1\)となる確率であり、その確率のパラメーターが\(\theta\)に入っている。
また、そのときに\(y\)が0になる確率と1になる確率を足すと1にならなければならないので、
\(P(y=1|x;_\theta)=0.7\)は\(P(y=0|x;_\theta)=0.3\)ということにもなる。
もっとわかりやすく書くと、\(P(y=1|x;_\theta)+ P(y=0|x;_\theta)=1\)になる。

 Decision Boundary

前提知識
\(h_\theta(x)= g(\theta^T x)\)
\(h_\theta(x) \geq 0.5 \rightarrow y = 1\)
\(h_\theta(x) \lt 0.5 \rightarrow y = 0\)

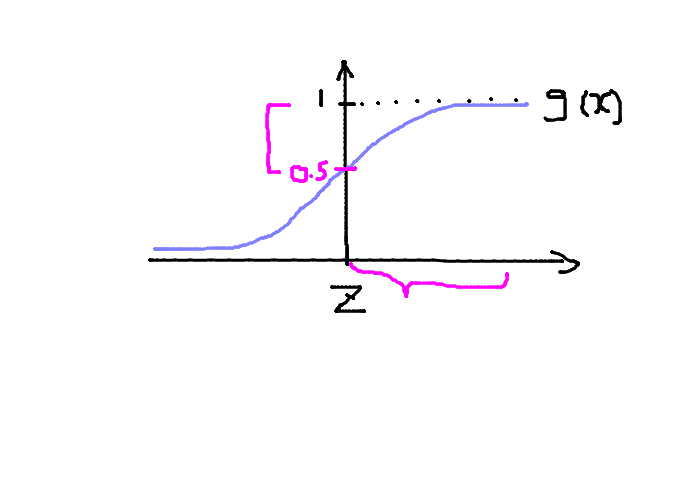
上記画像だと\(\quad z \geq 0\)のとき\(g(z) \geq 0.5\)となります。
\(z\)を展開すると\(\quad \theta^T x \geq 0\)のとき\(g(\theta^T x) \geq 0.5\)となります。

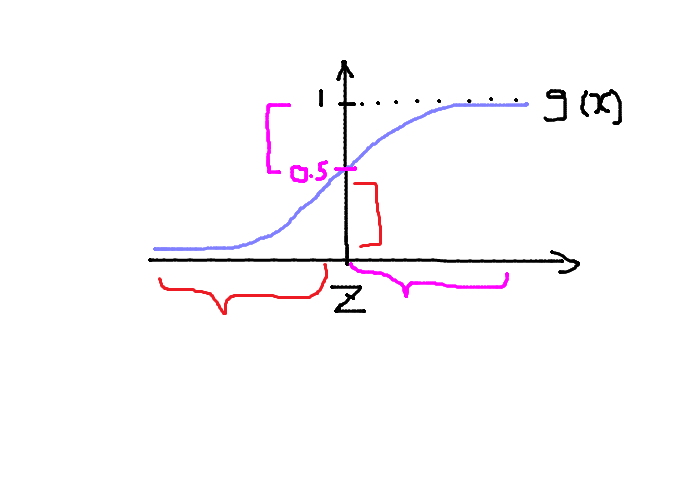
逆に上記の画像だと\(\quad z \lt 0\)のとき\(g(z) \lt 0.5\)となります。
\(z\)を展開すると\(\quad \theta^T x \lt 0\)のとき\(g(\theta^T x) \lt 0.5\)となります。

\(\theta = \left(
\begin{array}{ccc}
-3 \\
1 \\
1
\end{array}
\right)\)
\(y=1 \quad if \quad -3+x_1+x_2 \geq 0\)
\(-3+x_1+x_2 \geq 0\)
\(x_1+x_2 \geq 3\)
上記のような\(\theta\)が与えられたとき、\(x_1+x_2 \geq 3\)なら\(y=1\)になり
\(y=0 \quad if \quad -3+x_1+x_2 \lt 0\)
\(x_1+x_2 \lt 3\)になり\(y=0\)となる。
グラフにすると下記になる。

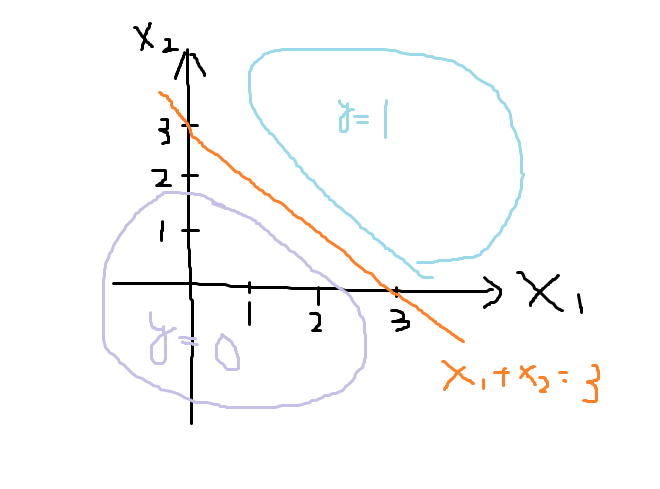
\(x_1+x_2 \geq 3\)の直線を決定境界と呼ぶ。決定境界によって\(y=0\)と\(y=1\)を分ける。
\(x_1+x_2 \geq 3\)上の値は\(h_\theta(x)=0.5\)になる。

さらに複雑にすると下記の画像のようになる。

Cost Function

ロジスティック回帰のコスト関数です。
\({J}(\theta) = \frac{1}{m}\sum_{i=1}^{m}\frac{1}{2} ({h}_\theta(x_i) – {y}_i)^2\\\)
\(Cost(h_\theta(x),y) = \frac{1}{2} ({h}_\theta(x) – {y})^2\)

1番目の\(\frac{1}{2}\)以降をコスト関数に代入します。しかし、これにはシグモイド関数が使われているため、非線形のグラフになり、非凸型グラフとなってしまう。
そのため、別のコスト関数を使用します。

\(Cost(h_\theta(x),y = -\log(h_\theta(x))) \qquad if \quad y = 1 \)
\(Cost(h_\theta(x),y = -\log(1 – h_\theta(x))) \qquad if \quad y = 0\)

\(y\)がコスト関数で支払うコストであり、0か1かによって\(\log\)の計算式が変わります。

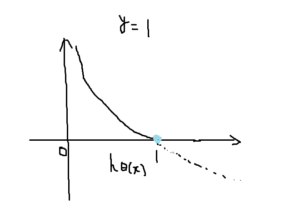
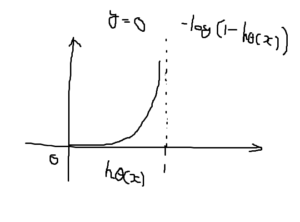
対数関数(下記画像)が登場し、仮説が\(h_\theta(x)=1\)を予測して\(y\)が実際に予測した値と同じならコストは0になります。
逆に\(h_\theta(x)=0\)が0に近づくとコストが急増して∞に近づいてしまいます。つまり、仮説が0を出力するなら\(y=1\)の可能性は0に等しくなります。
そして\(y=0\)と結論付けた後に\(y=1\)だった場合はこの学習アルゴリズムにペナルティを与えます。逆もまた然りです。

コスト関数の単純化と最急降下法

\(Cost(h_\theta(x),y = -\log(h_\theta(x))) \qquad if \quad y = 1 \)
\(Cost(h_\theta(x),y = -\log(1 – h_\theta(x))) \qquad if \quad y = 0\)

上記の2つの数式を簡単に書くと下記のようになります。
\(Cost(h_\theta(x),y) = -y\quad \log(h_\theta(x))) – (1 – y) \log (1 – h_\theta(x))\)

ここで注意なのが常に\(y=0or1\)の数値のみが入るということです。そうするとうまい具合に片方の項が0になるのでコンパクトになります。

これにより、初めに出てきたロジスティック回帰のコスト関数を一行で書き表せることができます。
\(J(\theta) = – \frac{1}{m} \sum_{i=1}^{m} [y^{(i)}\quad\log(h_\theta(x^{(i)})) + (1 – y^{(i)}) \log (1 – h_\theta(x^{(i)}))]\)

さらに最急降下法の関数と合わせると
\(\begin{align*} & Repeat \; \lbrace \newline & \; \theta_j := \theta_j – \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)}) x_j^{(i)} \newline & \rbrace \end{align*}\)
となります。

このアルゴリズム、どこかで見た覚えがありますね。そう、線形回帰のときに出てきたものと同じものです。では、ロジスティック回帰と線形回帰のアルゴリズムは同じものなのか？
答えは仮説の定義が違うということです。
線形回帰のでは
\(h_\theta(x)=\theta^T X\)でしたが、
ロジスティック回帰では
\(h_\theta(x)=\frac{1}{1+e^{-\theta^T x}}\)
となっています。そのため、実際には線形回帰の勾配降下法とは違うものとなります。

\(\theta = \left(
\begin{array}{ccc}
\theta_0 \\
\theta_1 \\
\theta_2 \\
\theta_n
\end{array}
\right)\)
とそれぞれ\(\theta_n\)を繰り返し処理して同時更新する必要があるが、ここではfor文による繰り返し処理よりも、ベクトル化による実装をしたほうがいいです。理由として、まとめて急降下させて更新することができるからです。

前回の講義で学んだFeature Scalingはロジスティック回帰でも適用できます。
ベクトル化した実装は以下の通りです。
\(h = g(X\theta)\)
\(J(\theta) = \frac{1}{m} (-y^T \log(h) – (1 – y)^T \log(1 – h))\)

Advanced Optimization

最急降下法よりもより高度な方法が登場。
ここでは共役勾配法、BFGS、L-BFGSを紹介しています。これらは最急降下法よりも収束が速く、学習率を自分で設定する必要がありません。その代わりに、処理が複雑になっています。今回の講義では触りだけ説明。

 Multiclass Classification: One-vs-all

多クラス分類についてです。1つのクラスvs全クラスというように分けてから決定境界を引いています。例えば3つのクラスを分類する時には1vs2and3,2vs1and3,3vs1and2と３つの決定境界を持ちます。

Ⅲ．Regularization

過学習(Overfitting)についてです。例として、家の大きさによって価値が決まるデータがあり、一次関数でアルゴリズムを作成すると、家の大きさがある程度大きくなると価値の上り幅が小さくなっていき、アルゴリズムに合わなくなっていきます。このことをアンダーフィッティング、別の言葉だとこのアルゴリズムはハイバリアンスを持つと言います。データにちょうど当てはまることをジャストライトと呼ぶみたいです。

要約すると、過学習は多すぎる特徴を持ち、学習させる仮説がトレーニングセットに適合しすぎたときに起こります。

そんな過学習を減らすためにはいくつかの方法があります。
1.特徴量を減らす
(1).手動で必要な特徴といらない特徴を分けていらない特徴を捨てる
(2).モデルセレクションを使用する(後の講義ででてくる)
2.正則化
(1).特徴は残すが\(\theta_h\)の値を減らす

Cost Function

正則化を含めたコスト関数についてです。

\(min_\theta \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)} )^2 + \lambda \sum_{j=1}^n \theta_j^2\)

パラメーターが増えた場合に\(\theta_1 ~\theta_n\)までペナルティを与え縮めるようにします。ペナルティは\(\theta_0\)から与えてもいいが、特に影響はないため慣例として\(\theta_1\)から与えます。\(\theta_j^2\)は\(\theta\)を二乗してねという意味の2です。また\(\lambda\)が大きすぎると全ての特徴を消去するほどに0に近くしてしまうため、残るのは\(\theta_0\)のみとなってしまい、直線のアルゴリズムになってしまいます(アンダーフィッティングを起こし、高いバイアスを持ってしまう)。

Regularized Linear Regression

正則化した線形回帰です。
パラメータ\(\theta_0\)は最適化の式では独立させますが、これは正則化のペナルティ対象外のためです。以下が式です。

\(\begin{align*} & \text{Repeat}\ \lbrace \newline & \ \ \ \ \theta_0 := \theta_0 – \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)})x_0^{(i)} \newline & \ \ \ \ \
\theta_j := \theta_j – \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2…n\rbrace\newline & \rbrace \end{align*}\)

そして、パラメータ\(\theta_j\)に関する式を変形すると

\(\theta_j := \theta_j (1-\alpha \frac{\lambda}{m})- \alpha \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)})x_j^{(i)}\)

この\(1-\alpha \frac{\lambda}{m}\)は通常1より小さい数値になります。
先生曰く、\(\theta_j (1-\alpha \frac{\lambda}{m})\)の部分は\(\theta_j\)に0.99をかけて少しづつ0に近づかせていると思ってもらって構わないらしいです。

正規方程式で書くと以下のようになります。

\(\begin{align*}& \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \newline& \text{where}\ \ L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}\end{align*}\)

Regularized Logistic Regression

正則化したロジスティック回帰についてです。
コスト関数は以下の式(\(\theta_0\)を除く)

\(J(\theta) = – \frac{1}{m} \sum_{i=1}^{m} [y^{(i)}\quad\log(h_\theta(x^{(i)}))) + (1 – y^{(i)}) \log (1 – h_\theta(x^{(i)})))] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \)

Ⅳ．おまけ

overfittingとunderfittingの違いについて自分なりにふとまとめておきたいと思ったので。
ますはoverfittingから。過学習という意味ですね。アルゴリズムとデータセットの適合率が99.9%とかはもう過学習になっていると思います。データセットのためのアルゴリズムになっていますし。
続いて、underfitting。読みかたは過小学習や未学習と呼ぶみたいです。こちらは過学習と逆で、アルゴリズムがあまりデータセットとは適合していない状態ということでしょうか。私がunderfittingの線形を見たときは適合しているようでしていない曖昧な線形でした。

プログラミング課題から
シグモイド関数\(g(z) = \frac{1}{1+e^{-z}}\)の実装は下記のようになりました。
\(1 / (1+exp(-z))\)
expは自然対数であるネイピア数(ここで言うeのこと)を底とする対数のことです。
exp(x)は自然対数のべき乗になります。
zにベクトルが入るときは./で各要素の除算をするようにしないといけない？

2×3という行列があるときに
\(size(A,1)\)とすると、Aの行数(2)を出力
\(size(A,2)\)とすると、Aの列数(3)を出力します。

Ⅴ．さいごに

week3を受講しましたが、week1とweek2に比べて難易度が跳ねあがったように思えます。今回は講義を聴きながら、その都度理解できているかの確認を含めてブログにメモをしてみました。その甲斐あってか、理解度は高まった気がします。プログラミング課題ですが、毎度のごとく難しいです。関数の理論自体は理解しているのですが、それをoctaveで実装するとなると、また違った難しさがあります。わかるところはすぐ実装できるのですが、細かい理論や計算は調べないと解けないレベルでした。難易度故か先生はシリコンバレーにいる機械学習エンジニア並みの理論知識を身につけたを言っていましたが励ましでしょうか…(先生、ほんとにこれ1週間で終わるレベルなのですか？(笑))

では、week4も頑張っていきます！