couresera machine-learning week5[学習メモ]｜ゆうのプログラミング部屋

Coursera Machine Learning
Week5【学習メモ】【機械学習】
スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。

機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース（1日1~2時間ペース？）としていますが、気にせずに理解できているか確認しながら進めていこうと思います。

Ⅰ．Neural Networks: Learning

Cost Function

ニューラルネットワークの目的関数です。
初めに用語の説明から。

\(K\)	出力レイヤーのユニットの総数
\(L\)	レイヤーの総数
\(S_l\)	ネットワークのレイヤー\(l\)に存在するニューロン総数の内、バイアスユニットを含めない数
\(S_L\)	出力レイヤーのユニットの総数

ここでは、ラベルが2つしかない「バイナリ(2値)分類」と「マルチクラス分類」を扱います。

・バイナリ分類では出力が0か1のみなので、出力ユニットは１つのみです(\(S_L=1\))。
それは、出力ユニットでは\(h_\theta(x)\)の計算をすることになり、実数となります。

・マルチクラス分類では、K個の異なる分類がある問題です(\(S_L=K\))(\(K\geq 3\))。
つまり、K個の出力ユニットがあり、仮説ではK次元のベクトルを出力することになります。

\((h_\Theta(x))_i\)の\(i\)は出力のベクトルの何番目かを表している。

以下がロジスティック回帰における正則化された目的関数(以前まで使用していた)と、正則化を含んだニューラルネットワークのコスト関数です。

\(J(\theta) = – \frac{1}{m} [ \sum_{i=1}^m y^{(i)} log(h_\theta (x^{(i)})) + (1 – y^{(i)}) log(1 – h_\theta (x^{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j ^2\)

\(J(\Theta) = – \frac{1}{m} [ \sum_{i=1}^m \sum_{k=1}^K y_k^{(i)} log(h_\Theta (x^{(i)}))_k + (1 – y_k^{(i)}) log(1 – (h_\Theta (x^{(i)}))_k)]\)
\(+\frac{\lambda}{2m} \sum_{l=1}^{L – 1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l + 1} (\Theta_{j,i}^{(l)} )^2\)

目的関数は予測値\(h_\Theta(x)\)と実数値\(y\)がどれだけずれているのかを測ったものでしたね。

誤差逆伝播法(BP)(重要)

計算方法について。

トレーニングセットが複数あるとします。
\({(x^{(1)},y^{(1)},…,(x^{(m)},y^{(m)}))}\)

次にすべての\(l,i,j\)の値に対して\(\Lambda^{(l)}_{i,j} := 0\)とします。
\(l,i,j\)は後の偏微分で使います。
\(l,i,j\)は、\(i\)番目のデータセットを使って計算したレイヤー\(l\)のアクティベーションユニット\(a^{(l)}_j\)における、目的関数\(J(\Theta)\)の偏微分が入ります。

次はFor文を使ってループ処理をします。\(i=1:m\)
以下Forループ内処理。

\(a^{(1)}\)の入力レイヤーのアクティベーションに対し、\(x^{(i)}\)をセット。
Set \(a^{(1)}=x^{(i)}\)
アクティベーション(関数)とは活性化関数のことで、ここではシグモイド関数を指す。

そこからレイヤーの数\(a^{(l)}\)を\(l=2,3,…,L\)と2~最後のLまでフォワードプロバケーションにてループで計算。
フォワードプロバケーションについては下記図参照。
\(z^{(j)}\)は活性化関数を通す前の値で、\(a^{(j)}\)は活性化関数を通した後の値です。
\(a^{(1)}\)は入力\(x\)であり、\(a^{(L)}\)は出力\(y\)を指します。

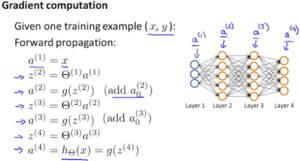
次に\(y^{(i)}\)を使用して、出力の誤差を計算します。
下記式。
\(\delta^{(L)}=a^{(L)}-y^{(i)}\)
\(a^{(L)}\)は仮説の出力結果で、\(y^{(i)}\)はターゲットにしている観測値です。

次に各レイヤーにおける誤差を求めます。
例だと\(\delta^{(L-1)},\delta^{(L-2)},…,\delta^{(2)}\)までを求める。以下式。
\(\delta^{(l)}=((\Theta^{(l)})^{T})\delta^{(l+1)}.*a^{(l)}.*(1-a^{(l)})\)
レイヤー\(l\)のデルタ値は、次のレイヤーのデルタ値にレイヤー\(l\)のシータ行列を乗算することによって計算されます。次に、これに\(g’\)またはg-primeと呼ばれる関数を要素ごとに乗算します。これは、\(z\)で指定された入力値で評価された活性化関数\(g\)の導関数です。

\(g\)はシグモイド関数であり、\(g’\)はそれを微分した関数です。
計算式は\(g'(z)=g(z)(1-g(z))\)ですが、
わかりやすくすると\(g'(z^{(l)})=a^{(l)}.*(1-a^{(l)})\)になります。

各偏微分値を足していきます。
以下式。
\(\Delta^{(l)}_{i,j}:=\Delta^{(l)}_{i,j}+a^{(l)}_j*\delta^{(l+1)}_i\)
ベクトル化して求めると下記式変更。
\(\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}_i(a^{(l)})^{T}\)

最後にパラメータ(上の式)とバイアス(下の式)の値を更新します。
\(D^{(l)}_{i,j} := \dfrac{1}{m}\left(\Delta^{(l)}_{i,j} + \lambda\Theta^{(l)}_{i,j}\right) (if \quad j \neq 0)\)
\(D^{(l)}_{i,j} := \dfrac{1}{m}(\Delta^{(l)}_{i,j})\) \((if \quad j = 0)\)

ブログには書いていませんが、用語をメモ
ニューロン(\(a^{(2)}_2\)とかの丸い中にはいっているあれ)=ノード
信号(\(z\)から\(a\)に変わるときの綱渡し)=エッジ

Backpropagation Intuition

続けて、誤差伝播法についてです。
二値分類にした場合\((K=1)\)は正則化なしになり以下の式になります。
\(cost(i) =y^{(i)} \ \log (h_\Theta (x^{(i)})) + (1 – y^{(i)})\ \log (1 – h_\Theta(x^{(i)}))\)
上の方に記述した正則化ありのニューラルネットワークのコスト関数と比べると\(\lambda=0\)になるため、正則化項がなくなっています。

\(\delta^{(l)}_j\)は\(a^{(l)}_j\)(レイヤー\(l\)の\(j\)ユニット)の誤差です。

専門的に言うと、隠れ層や出力層\(h_{(x)}\)の計算に影響を与え、結果として全体のコスト関数に影響を与えるためにどれだけウェイトを変更すればいいかの指標です。

\(\delta^{(l)}_j\)はより正確に言うと、コスト関数を偏微分した値です。
以下式。
\(\delta_j^{(l)} = \dfrac{\partial}{\partial z_j^{(l)}} cost(i)\)\((j\geq 0)\)

Andrew先生の説明資料(coursera machine-learningより)です。

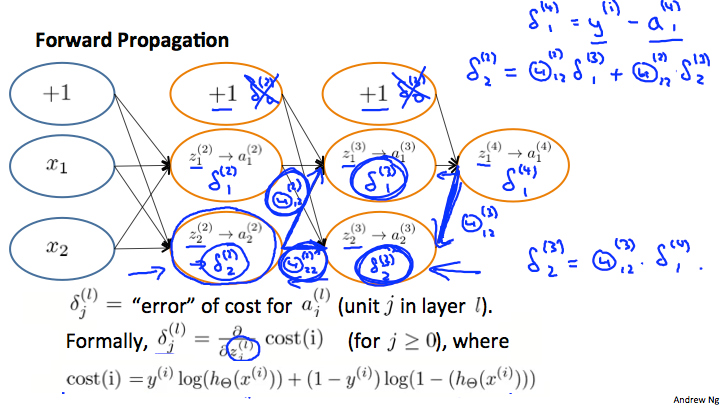
上の資料を説明すると、フォアワードプロパゲーションをした後にバックプロパゲーションにて\(\delta^{(l)}_j\)をどのように求めるかを記述しています。以下式。
\(\delta^{(2)}_2=\Theta^{(2)}_{1,2}\delta^{(3)}_1+\Theta^{(2)}_{2,2}\delta{(3)}_2\)
\(\delta^{(3)}_2=\Theta{(3)}_{1,2}\delta^{(4)}_1\)
というように、求めたい\(\delta^{(l)}\)の\(l+1\)レイヤーに向けたエッジ(\(\Theta\)のこと)と
\(l+1\)レイヤーの\(\delta^{(l+1)}\)をそれぞれ積と和で計算すると求めることができました。

ここでは計算しませんでしたが、バイアスユニットの\(\delta\)の計算はバックプロパケーションのアルゴリズムをどう定義(実装)するかで変わります。

Ⅱ．Backpropagation in Practice

Unrolling Parameters

octaveでのパラメータの展開方法についてです。
ロジスティックでは微分項(gradient)はベクトルでOKでしたが、ニューラルネットワークではベクトルではなく、行列としてパラメータを扱うことになります。そこで、どうベクトルと行列との変換を行うかが今回のテーマです。例として以下を扱います。

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

\(thetaVec\)では、\(Theta1\sim 3\)の全要素を取り出してアンロール(展開)し、全要素を1つの長いベクトルに入れています。\(deltaVector\)も同じです。
また、一度1つのベクトルに入れたのを行列に戻したくなったら

Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

このようにreshapeを使って戻すことができます(例ではtheta1=10*11(1~110番目まで),theta2=10*11(111~220番目まで),theta3=1*11(それ以降)の行列)。

下記は実装方法です。

\(thetaVec\)がパラメータ(ベクトル)として与えられています。
なので初めに\(thetaVec\)を使って、reshape関数を使い、行列に復元します。
その後\(D\)をアンロールします(gradientVecを得るため)。

・行列表現の利点
パラメータを行列で保存しておけば、フォワード/バックプロバケーションをする時や実装をベクトル化する時に行列の方がやりやすい。

・ベクトル表現の利点
thetaVecやDVecにする利点は、アドバンスド(高度)な最適化アルゴリズムを使う時にパラメータを1つの大きなベクトルにアンロール(展開)してあることを仮定としている事が多い。

Gradient Checking

誤差逆伝播法は度々バグが発生してしまうため、チェックのためGradient Checkingを実装します。
\(\theta\)パラメータが実数の時は以下の式になります。

\(\dfrac{\partial}{\partial\Theta}J(\Theta) \approx \dfrac{J(\Theta + \epsilon) – J(\Theta – \epsilon)}{2\epsilon}\)

パラメータの値にイプシロン\((\epsilon)\)(差分)を増減させ微分(傾き)の近似値を計算します。
\(\approx\)はニアリーイコールの意味です。

\(\theta\)パラメータが行列の時には以下の式になります。

\(\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) – J(\Theta_1, \dots, \Theta_j – \epsilon, \dots, \Theta_n)}{2\epsilon}\)

イプシロン\(\epsilon\)は\(10^{-4}\)くらいが良いが、小さすぎる値を使用すると数値的な問題が起こる可能性があるため注意!

octaveで数値的グラディエントチェッキングを実装する時のコード例を下記記載。

epsilon = 1e-4;
for i = 1:n, //アンロールしたパラメータを使用
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

数値的グラディエントチェッキングの実装
１．DVecを計算するために、バックプロパケーションを実装。
２．gradApproxを計算するために、数値的グラディエントチェッキングを実装。
３．DVecとgradApproxが似た値か確認。つまり近似値とバックプロパケーションから得た微分が(ほぼ)等しいか確認(小数点以下数桁で正しければ〇)。その後、最急降下法とかに使用。gradApprox\(\approx\)DVec
４(重要)．数値的グラディエントチェッキングを切る(数値的グラディエントチェッキングは計算が遅いコードのため)。

Random Initialization

ランダム初期化についてです。
最急降下法や最適化アルゴリズムを走らせるときにはパラメータ\(\theta\)の初期値を決めていました。ロジスティック回帰を実装する時は、全てのパラメータの初期値に0を入れていましたね。しかし、ニューラルネットワークで同じことをしてしまうと、各ユニットのウェイトが同じになってしまい、関数を計算する時も結果として同じ値になってしまうという不具合が起きてしまいます。

そこで\(\Theta\)を\(-\epsilon\)から\(\epsilon\)の範囲でランダムな値で初期化します (Symmetry Breaking)。

ちなみに、ランダム初期化での\(\epsilon\)は前回の数値的グラディエントチェッキングで出てきたものとは無関係です。

対称ウェイトと呼ばれることもあり、ウェイトが全て同じになってしまうために起こる不具合です。そのため、このランダム初期化で対称性を解決するというわけです。

octaveで実装するときは以下のようなコードが例となります。

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

rand(x,y)により、0から1までのランダムな実数の行列を初期化しています。

ニューラルネットワークまとめ

ニューラルネットワークの実装には大きく分けて6段階あります。
0．ニューラルネットワークのアーキテクチャを選択する。
ニューラルネットワークの実装前にやらなければならないことがあります。それは、ニューラルネットワークのアーキテクチャを選択することです。
ここで言うアーキテクチャとは、ニューラルネットワーク同士の接続のパターンであり、いくつ隠れ層とそのユニットを選択するかということです。

入力ユニット数の決め方は、特徴\(x^{(i)}\)次元数で決定する。
出力ユニット数の決め方は、マルチクラスの分類問題を扱う場合は、クラスの数によって決めることができます。

隠れ層数については基本的には1つにします。もしも2つ以上にする場合には、隠れユニット数は全隠れ層で統一します。
では、隠れ層ユニットの数はどのように決めればよいかと言うと、\(x\)の次元または特徴数と同程度~2,3,4倍などが望ましいです(多ければ多いほど良かったりする)。

１．ニューラルネットワークをセットアップして、重さの値をランダムに初期化する。

２．\(h_\Theta(x^{(i)})\)を計算するため、フォワードプロバケーションを実装。

３．コスト関数である\(J_\Theta\)を計算するコードを実装する。

４．\(J_\Theta\)の偏微分を計算する誤差逆伝播法(BP)を実装。

５．Gradient checkingを使って誤差逆伝播法(BP)が機能するかを確認し、BPを切る。

６．最急降下法や他のアルゴリズムを使って最小化を試みる。

ニューラルネットワークの場合、\(J(\theta)\)は非凸関数なので理論上局所的最適解に陥る可能性があるが、そこまで問題にはならずにちゃんと最適な局所最小を見つけてくる。

Ⅲ．おまけ

プログラミング課題を進めるにあたってメモ
\(\Delta\)は大文字デルタの意味で、小文字デルタ\(\delta\)の累積になります。
\(\Theta\)とユニットの数を合わせるために、\(\Theta\)の一列を削除する必要がありましたが、\((:,2:end)\)で行列の一列目を削除することができます。

Ⅳ．さいごに

長いweek5が終了しました。。。ネットでの反応を見ていると、week5が一番の鬼門と言われているのがわかりました。ただそれだけに、ニューラルネットワークについて基礎的な部分は学ぶことができましたし、人間の脳を模倣するってめちゃくちゃ面白い内容でした。一番興味を惹かれる内容だったと思います。内容が非常に濃かったので、一度さらっと復習してからweek6に進もうと思います。

引き続き頑張っていきましょう！

couresera machine-learning

Coursera Machine Learning / week5【学習メモ】