Coursera Machine Learning
Week1【学習メモ】【機械学習】

スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。

機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース（1日1~2時間ペース？）としていますが、気にせずに理解できているか確認しながら進めていこうと思います。

Ⅰ．Introduction

機械学習の定義

A computer program is said to learn from experience E with respect to some task T and some performance measure P if its performance on T, as measured by P, improves with experience E.

上記の定義は以下のP,T,Eの要素からなる。

教師あり学習

・人間により正しい答えが与えられる

・分類問題：結果を離散出力で予想。例：悪性腫瘍か良性腫瘍か

・回帰問題：連続値・実数値を予想。例：向こう3カ月間の土地値段の推移

教師なし学習

・人間により答えが与えられない

・クラスタリング：データに内在するグループ分けを見つける。例：遺伝子タイプや銀河の成り立ちなど

・カクテルパーティー問題：2人での会話を1人1人に分ける。

Ⅱ．Linear Regression with One Variable

線形回帰モデルの式について

\(h\)はHypothesis(仮説)の略で\(\theta\)はパラメータを意味します。

\( h_\theta(x) = \theta_0 + \theta_1x\ \)
\( y = c + a(x)\)と書いた方が馴染み深いでしょうか。

\(x\)が0の地点の\(y\)の値を\(\theta_0\)、傾きを\(\theta_1\)としています。
つまり直線で表せることができます。シンプルですね。

ちなみに\(y\)は従属変数、\(x\)は独立変数と言うそうです。
今回の例で言うと、家の大きさによって価値が決まるというのでは家の大きさ(独立変数)によって価値(従属変数)が決まると言えます。

下記は機械学習の図です。

 

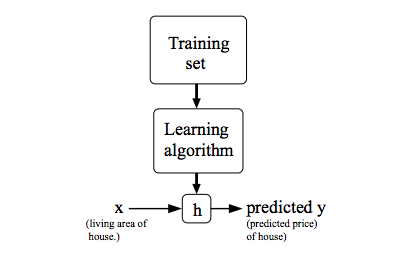
コスト関数

コスト関数の式は下記のようになります。

\({J}(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m} ({h}_\theta(x_i) – {y}_i)^2\\\)

mはデータセットの数。
\(1/2\)というこの数字に今は意味はありません。後々計算する時にいいようになります。
\(h_\theta(x_i) – y_i\)での\(x_i\)と\(y_i\)はデータセットのi番目の大きさ\(x_i\)と価格\(y_i\)を指しています。
\(h_\theta(x_i)\)は先ほど記した仮説であり、\( h_\theta(x) = \theta_0 + \theta_1x\ \)です。初期値と傾きと\(x\)をかけたものでしたね。

この仮説と\(y\)の差分を求め、m個のデータ数分だけ足し合わせる、その結果データセットとの差が大きければ間違った\(\theta\)であり、小さければ適切な\(\theta\)と言えるでしょう。
2乗については差分がマイナスにもプラスにもなるのでマイナスだった場合に打ち消す用だと考えています。

平均二乗誤差とも呼ばれ、\({J}(\theta_0,\theta_1)\)を最小化します。

最急降下法

\({J}(\theta_0,\theta_1)\)が最小になるように動かしていくことが目的。

以下の計算式でパラメータの最適化を図る。尚、収束するまで繰り返される。
\(Parameter: \theta_0, \theta_1\\\)

\(\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)\)
:=は代入の意味。
\(\alpha\)は学習レートで、値が小さいと一度に進む距離が少なく、値が大きいと一度に進む値が大きい。
値が小さい→進む距離が小さく、最小値に辿り着くまで時間がかかる。
値が大きい→進む距離が大きいため、最小値から遠ざかる危険性。

偏微分・・・高校のときに学んだような単語です。偏微分とは何か曖昧なまま進めるのも嫌なので調べていきます。
\(\partial\)はラウンドと呼びます。\(\partial\)は分母にある変数で偏微分してねっていう意味です。
偏微分の定義は「偏微分とは，多変数関数を「特定の文字以外定数だとみなして」微分したもののこと」です。例えば、定義で言う特定の文字を\(x\)だとすると\(x\)以外の\(y\)とかの変数は定数と見なして無視してねということになります。

じゃあ微分とは何ぞやというと、変化量のことです。
簡単な例だと、微分(x)のxが1ずつ変化するときの微分(x)の変化量(傾き)のことです。
偏微分も同じく、変化量(傾き)を求めるためのものです。
なので、上記の式から\(\theta\)を偏微分するということは\(\theta\)の傾きを求めることを意味します。この傾きを使ってゴールを目指していきます。

初期位置を決めてから最急降下法をスタートしますが、開始位置が適切でないと最初から局所的最適解(local optima)になってしまい、大域的最適解(global optima)まで辿り着きません。言い換えると局所的最適解は目に見える範囲内で最小にいると感じるが、実際の最小ポイントは今いるポイントからは見えない向こう側にある大域的最適解という場所にあります。また、局所的最適解か大域的最適解のポイントにいると接戦の角度がなくなるため、更新が止まってしまいます。

コスト関数+最急降下法

コスト関数と最急降下法の式を合わせると下記のようになる。

\(temp_0 := \theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}({h}_\theta(x_i) – y_i)\)

\(temp_1 := \theta_1-\alpha\frac{1}{m}\sum_{i=1}^{m}({h}_\theta(x_i) – y_i)x_{i})\)

\(\theta_0 = temp_0\)

\(\theta_1 = temp_1\)

最急降下法は\(\theta_0,\theta_1\)を同時に更新しなければなりません。そのため、tempに代入しています。同時に更新しないと意図しない結果になる可能性があるためです。

Ⅲ．まとめ

今回は家の価値に影響を与える変数が一つ(大きさのみ)であったため、単純線形回帰といいます(多数ある場合は多重線形回帰と言う)。単純線形回帰ではコスト関数を使って最小となる\(\theta\)値を探すことです。探し方は微分をすることで傾きを算出し、学習率をつかいながら\(\theta\)値を改善していきます。

Ⅳ．さいごに

この講義を受講してみて、思いのほかweek1を終わらせるのに時間がかかりました。高校のときに英語を少し勉強していたため、なんとなく読解はできますがそれでも難しいです。パッと見てわからなそうなら躊躇いなく翻訳にかけていこうと思います。講義の内容自体はとてもわかりやすくてスッと入ってきます。高校以来数学触っていなかったけどとても理解しやすい。この調子でweek2もやっていきます。