Coursera Machine Learning
Week8【学習メモ】【機械学習】
スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。
機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース(1日1~2時間ペース?)としていますが、気にせずに理解できているか確認しながら進めていこうと思います。
Unsupervised Learning
Unsupervised Learning: Introduction
クラスタリングアルゴリズムという新しい言葉が出てきました。
教師なし学習では、ラベルのないデータセット(正解のないデータ)が与えられ、データ内の「構造」を見つけるように求められます。
K-Means Algorithm
K-Meansと呼ぶクラスタリングのアルゴリズムについてです。
K-Meansアルゴリズムは2つの入力を受け取ります。
・パラメータ\(K\)=データの中から見つけたいクラスタの数(どうやって選ぶかは後述)
・ラベルのないトレーニングセットを受け取る(\(x\)だけ)
その後以下ステップにより実施。
1.ランダムに\(K\)個のクラスタの重心を選ぶ
重心は\(\mu\)で、\(n\)個のベクトルで表すことができます。
\(\mu_1, \mu_2, \cdots \mu_K \in \mathbb{R}^n\)

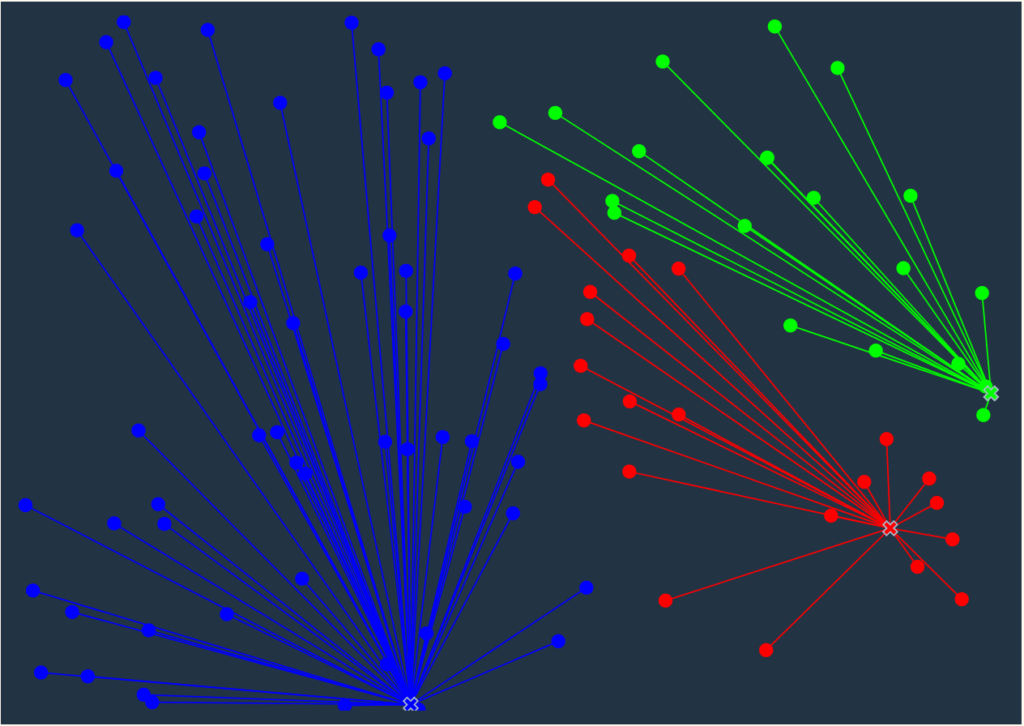
上記の画像だと、重心は3個あります。なので、
\(\mu_1, \mu_2, \mu_3 \in \mathbb{R}^3\)
と表すことができるのではないでしょうか。
2.各データサンプル\(x^{(i)}\)のラベル\(c^{(i)}\)を決める
各データ\(x^{(i)}\)に対して最も距離が近いクラスタを割り当てます。例として、4つ目のデータ\(x^{4}\)に一番近いクラスタが\(\mu_2\)の場合は、\(c^{(4)}=2\)と表せます。
\(c^{(i)} := K\)
3.クラスタ重心の移動
それぞれのクラスタの重心を各データの平均を計算した場所に移動します。
クラスタの重心に割り振られたデータがない場合は、その重心を取り除きます。そうすると\(K-1\)個のクラスタとなります。

そして、2と3を繰り返していくとクラスタの重心が移動しなくなります。
ですが、回数が実は決まっているみたいです。
Optimization Objective
K-Meansのコスト関数(目的関数)についてです。
教師なし学習でもコスト関数があります。教師なし学習であってもコスト関数を持つ理由は、以下の2点です。
・K-Meansの最適化の目的関数が何かを知ることは学習アルゴリズムをデバッグする助けとなるため。K-Meansがちゃんと走っているか確認できるから。
・K-Meansがより良いクラスタを見つける助けに出来るか、どう局所最適を避けるかの助けになるため
ここで変数の整理。
・\(c^{(i)}\)・・・\(x^{(i)}\)が現在どのクラスタに割り振られているのかのインデックスを見るための変数。
・\(\mu_k\)・・・クラスタ重心\(K\)の場所を表しています。
K-Meansでは大文字の\(K\)をクラスタの総数を表すのに使い、小文字の\(k\)でクラスタ重心のインデックスを表しています。小文字の\(k\)は\(1~k\)までの数字となります。
・\(\mu_{c^{(i)}}\)・・・クラスタ重心のうちサンプル\(x^{(i)}\)に割り振られているものを表す。
例として、\(x^{(i)}\)がクラスタ重心5に割り振られているとき、\(x^{(i)}→5\)と表すことができ、\(c^{(i)}=5\)になります。結果、\(\mu_{c^{(i)}}=\mu_5\)と表せます。\(c^{(i)}\)の部分を代入したみたいです。
K-Meansのコスト関数は以下の式です。
この目的関数を最小化します。クラスタからの距離の二乗の和です。
\({J(c^{(1)},…,c^{(m)},\mu_1,…,\mu_K) = \frac{1}{m} \sum^m_{i=1} ||x^{(i)} – \mu_{c^{(i)}}||^2}\)
\(x^{(i)}\)はトレーニングサンプルの\(x^{(i)}\)の位置で、\(\mu_{c^{(i)}}\)がサンプル\(x^{(i)}\)が割り振られたクラスタ重心の位置です。
Random Initialization
最初の重心をどのようにランダムに選択するかです。
K-Meansをランダムに初期化する方法です。
1.クラスタ重心の数\(K\)はトレーニング手本の数\(m\)よりも小さく設定しなくてはいけません。
2.\(K\)個のトレーニング手本をランダムに取り出します。
3.\(\mu_1\)から\(\mu_k\)にこれらをセットします。
以下K-Meansをランダムに初期化する例です。
1.\(K=2\)と設定します。
2.2個のトレーニング手本をランダムに選び、その真上にクラスタ重心を置きます。
一見良さそうな初期化の方法に見えるが、例での設定だとランダムに2個のトレーニング手本の上にクラスタ重心を置くが、すぐ近くの隣り合ったトレーニング手本を選んでしまうこともあり得るので、本当はあまりおすすめしない手法です。
ではどうすれば良いかというと、K-Meansを50回から1000回ほど実施して、コスト関数が最小の結果を選択するといいみたいです。
K-Meansは最初のステップである「ランダムにクラスタの重心を決定」にランダム性があるため、局所最適解に陥りやすいです。よりよい解を得るために以下のことをするらしいです。
ちなみに\(K\)が2~10個くらいならこの方法を実施すると良い解を求めることができますが、\(K\)が100個とかだとこの方法を試してもあまり効果は薄いみたいです。そのときは初めのランダム初期化で既に良い解が得られることが多いそうです。
Choosing the Number of Clusters
クラスタ数\(K\)の決め方。
どうすれば最適なクラスタ数を決められるかという話です。
可視化した結果を見てか、クラスタアルゴリズムの結果を見てか、その他何かを見て手動で選ぶという方法です。
なぜ、クラスタの総数を選ぶのが簡単ではないかというと、そもそもにデータにいくつのクラスタがあるのかが曖昧なことが多いからです(データセットを見てある人は\(K=4\)と見えるし、ある人は\(K=2\)と見える)。これはラベルという正確な回答が与えられていないからです。
一般的にはエルボー法と呼ばれる手法を使用することが多いです。
2次元のグラフで横軸にクラスタ数、縦軸にコスト関数の結果をとり、曲線が緩やかになった点(エルボー(肘のように見える場所))に決める方法です。
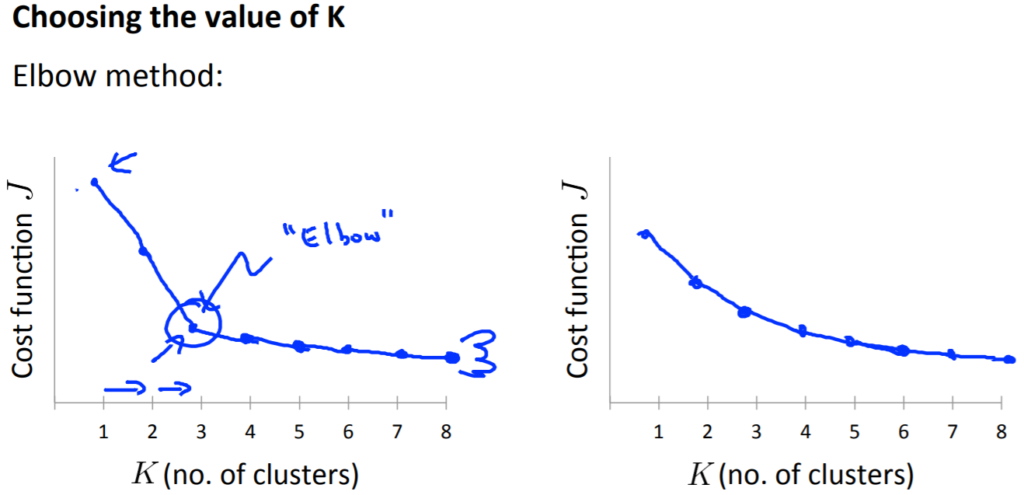
上記の画像の左のグラフでは、\(K=3\)まで急激に減少しており、そこから緩やかな現象になりました。まるで肘のように。なので、左のグラフでは\(K=3\)を選択することになります。
しかし、左のグラフのように上手くいく回数と同じくらい、右のグラフのような結果になるときがあります。右のグラフではどこが肘になっているか分かりづらいため、結果としては失敗です。
総合的にみると、このエルボー法は一発試してみる価値はあります。ただ、どんな問題にも上手くいくとは限らないと注意が必要みたいです。
目的に応じてクラスタ数を決める方法もあります。例としてあるように、Tシャツビジネスをするにあたり、サイズを多くするか少なめにして売るかをあらかじめ考えることにより、種類数\((K)\)を決めるなどです。
つまり、どういう目的でK-Meansを実行しているのかを考えることが大切です。
Ⅱ.Dimensionality Reduction
Motivation I: Data Compression
次元削減についての説明です。
なぜ、次元圧縮をすると、データを圧縮してより少ないメモリや容量になり、学習アルゴリズムのスピードアップにもつながります。
以下2Dから1Dへと次元削減。
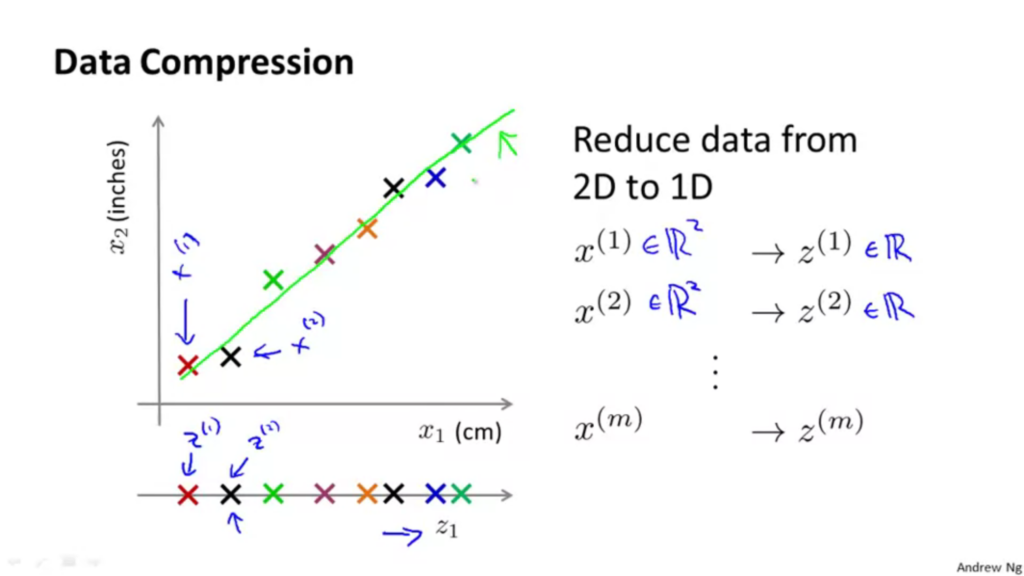
\(x\)に含まれている二つのベクトルを\(z\)一つで表しています。
以下3Dから2Dへと次元削減。
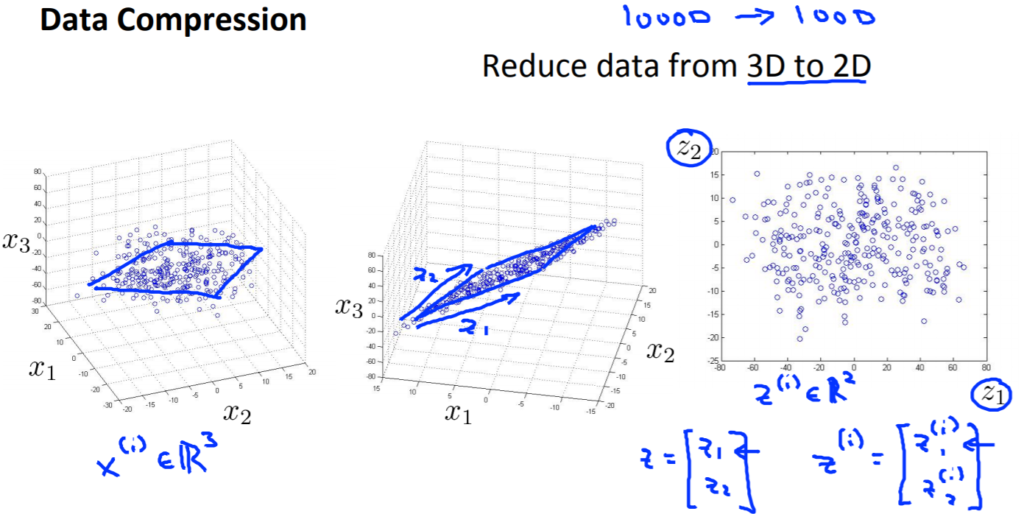
こちらは\(z_1\)と\(z_2\)の2Dで表示しています。
Motivation II: Visualization
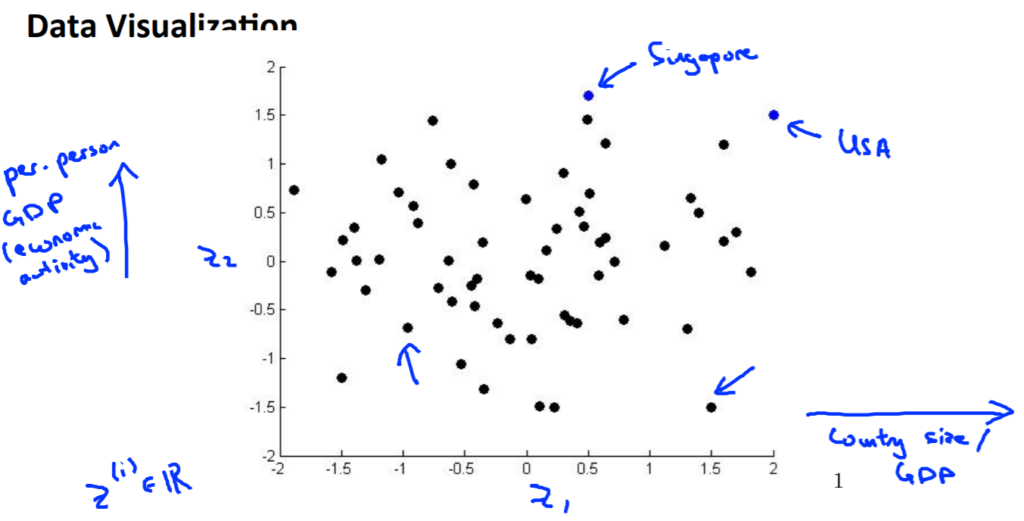
次元削減のメリットとして可視化についてです。
例として、50Dある特徴を2Dにしたら見やすいし把握しやすいよねということです。
以下参考図。
Principal Component Analysis Problem Formulation
主成分分析(PCA)について。
PCA (Principal Component Analysis)は主成分分析とも呼ばれ、1番人気で1番良く使われている(らしい)次元削減で人気のあるアルゴリズムです。
それは、元のデータ\(x\)の次元\(n\)でそれを\(k\)まで削減したいとき、PCAは\(n\)次元で投射誤差を最小にするベクトル\(k\)を見つけます(データを射影する\(k\)次元)。
PCAのゴールは、例で挙げると2Dから1Dへと次元削減する時にベクトル\(\mu_i\)を探すと言えます。\(\mu_i\)は\(R^{(n)}\)ベクトルであり、例の場合だと\(R^{(2)}\)と表せます。投影誤射を最小化するようなデータの投影先の方向を持つベクトルです(このベクトルは正でも負でも引かれている線は同じなので関係ない)。
ちなみに、線形回帰とPCAは全く別のアルゴリズムです(グラフが似ているため勘違いする)。
線形回帰(左の図)では、ある特徴\(x\)を入力として、ある変数\(y\)を予想しようと試みる。
点と直線との距離による二乗誤差を最小化するような直線をフィッティングする。
青い線を垂直に書いたが、それは点と仮説が予測した値との垂直な距離となっています。
一方、PCA(右の図)では青い線の大きさを最小化します。線形回帰と違い、角度をつけて青い線は書かれており、これは点と赤い線との直行した最短距離を表している。
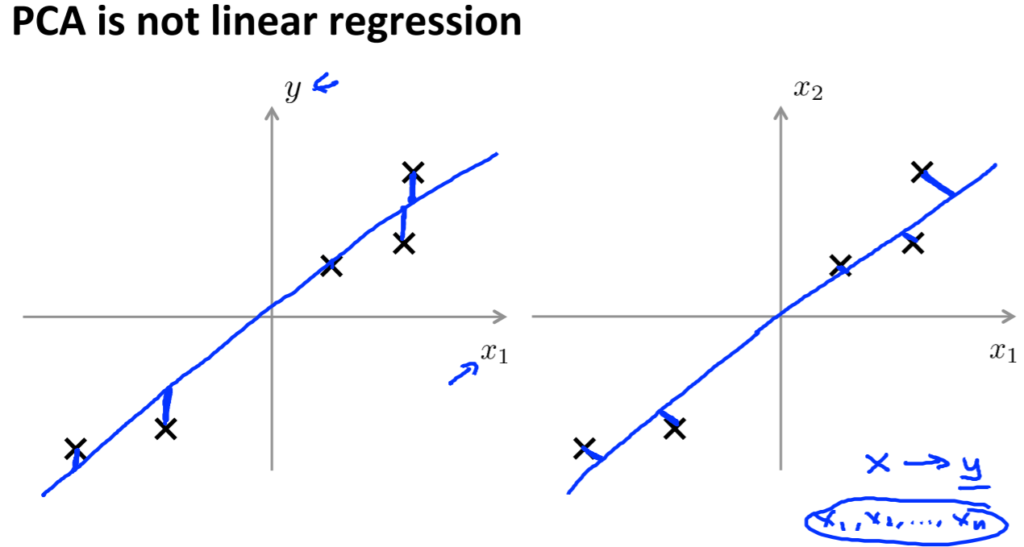
線形回帰では、変数\(y\)が予測しようとする変数として存在します。\(x\)を使い、\(y\)を予測しようとします。
PCAでは\(y\)はないため、\(x_1\)から\(x_n\)までの等しく扱われる特徴があります。
Principal Component Analysis Algorithm
主成分分析のアルゴリズムです。
\(n\)次元から\(k\)次元への削減方法。
1.データの前処理(必ずやらなくてはいけない)
平均標準化を必ず行います。データによってはFeature Scalingも実行します(教師あり学習とほぼ似ているがラベルなしデータの\(x_1\)から\(x_m\)に対してだけ違う)。
平均標準化のために、まず各特徴の平均を計算する必要があります。そして、各特徴\(x\)を\(x-\mu\)(x-平均)に置き換えます。そうすることで\(x\)は平均0となります。
\(\mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)}\)
上記の式で相加平均を求めて、\(x_j^{(i)}\)を\(x_j^{(i)}-\mu_j\)に置き換えて差分を計算します。
もしも特徴が異なるスケールであった場合、各特徴が比較できる範囲になるようスケールする必要があります。
Feature Scalingについてはweek2参照。
Coursera Machine Learning / week2【学習メモ】
2.共分散行列を計算する。
\(\sum = \frac{1}{m}\sum^n_{i=1}(x^{(i)})(x^{(i)})^{\mathrm{T}}\)
左項の記号はギリシャ文字の大文字シグマであり、行列を表します。右項の和を表すのとは違うので注意。
Octaveでは以下のコードで求められます。
Sigma = (X'*X)/m;
次にsingular value deconvosition関数(特異値分解)に先ほど計算した共分散行列を放り込むと求められます。
[U,S,V] = svd(Sigma);
ちなみに、svdの代わりにeig(Sigma)を使用しても同じ結果を返します(svdの方が少しだけ数値計算的に安定する)。
svdの引数であるSigmaは\(n*n\)の行列です。これは、\((X’*X)\)において\(X\)はn×1で\(X’\)は1×nであるため、\((X’*X)\)はn×nになる。
[U,S,V]のうち必要なものはUだけです。またUもn×nの行列になります。
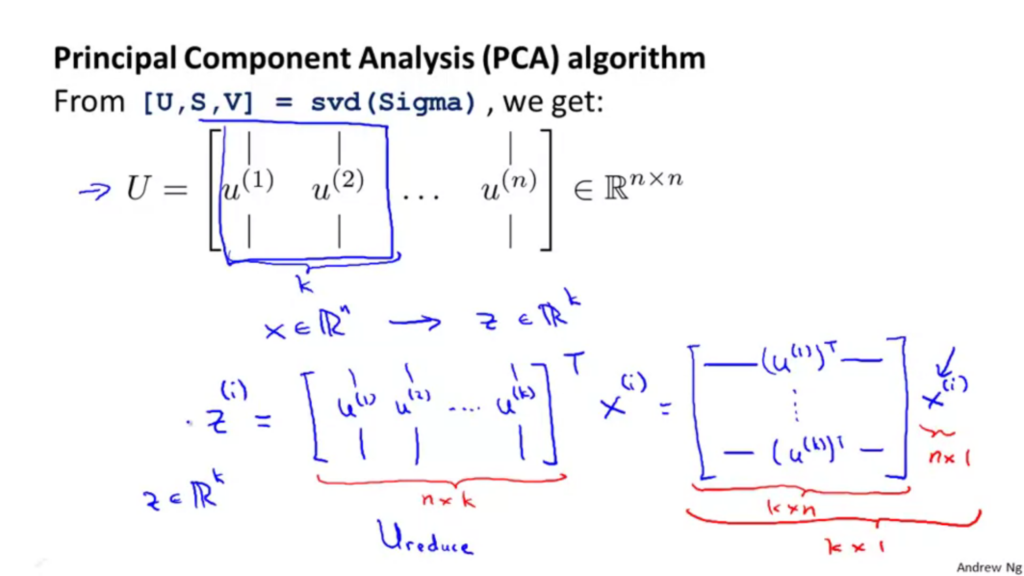
上記の図では、n次元からk次元へと削減したいときには、まず\(U\)の行列から最初のk本のベクトルをとり、\(\mu_1\)から\(\mu_k\)までを取得する。
それを、\(x\in R^{n}\)から\(z\in R^{k}\)へとする。
\(\mu_1\)から\(\mu_k\)までの行列を\(U_{reduce}\)と名前を付けた行列とします。この行列はn×kの行列です。
次に\(z=U_{reduce}^{T}x\)とするとベクトル\(z\)を取得することができる。詳しく見ると、\(U_{reduce}^{T}\)はk×nの行列で、\(x\)はn×1の行列であるため、行列\(z\)はk×1となります。
尚、上記の画像をOctaveでまとめると以下のようになります。
Sigma = (1/m)*X'*X; [U,S,V] = svd(Sigma); Ureduce = U(:,1:k); z = Ureduce'*x;
Reconstruction from Compressed Representation
PCAで削減された次元を元に戻す方法です。
X_approx = Z*U(:,1:k)';
これにより、\(z\)(m×k次元)から\(x_{approx}\)(m×n次元)に復活することができます。
Choosing the Number of Principal Components
次元\(k\)をいくつまで削減すべきかを説明しています。
次元を削減した時に、どれだけ分散が保持できるかを評価基準とします。
下記の平均射影自乗誤差を分散の総和を使って計算します。
平均射影二乗誤差
\(\frac{1}{m} ||x^{(i)} – x^{(i)}_{approx}||^2\)
分散の総和
\(\frac{1}{m} ||x^{(i)}||^2\)
平均射影二乗誤差を分散の総和で割ると、どれだけ分散が保持できるかを算出できます。
\({{\frac{\frac{1}{m}\sum^m_{i=1} ||x^{(i)} – x^{(i)}_{approx}||^2}{\frac{1}{m}\sum^m_{i=1}||x^{(i)}||^2}}}\leq 0.01\)(1%)
例として、上記の式が0.01(1%)以下にしたいとすると、「99%の分散を保持できる」という呼び方になります。
一般的には95%(0.05)から99%(0.01)が良く使われるみたいです。
では、削除する\(k\)次元をどのように算出すればよいか。
それは[U,S,V] = svd(Sigma)を使用します。
このうちのSはn×nの正方行列であり、対角成分以外はすべて0になります。
以下式を使用すると\(k\)の値を求めることができます。
\({variance \hspace{3pt} explained = 1 – \frac{\sum^k_{i=1}S_{i,i}}{\sum^n_{i=1}S_{i,i}}}\leq 0.01\)
または
\({variance \hspace{3pt} explained = \frac{\sum^k_{i=1}S_{i,i}}{\sum^n_{i=1}S_{i,i}}}\geq 0.99\)
または
\({{variance \hspace{3pt} explained = 1 – \frac{\sum^m_{i=1} ||x^{(i)} – x^{(i)}_{approx}||^2}{\sum^m_{i=1}||x^{(i)}||^2}}}\leq 0.01\)
以下図参照。

上記式の真ん中の式を使用した場合、svd関数を一度使用すればS行列を取得することができるので、それを使用して、0.99(99%)以上分散を保てる最小の\(k\)値を見つける方法だと効率がいい(k=3のときは対角成分3つ目までが分子で、対角成分すべてが分母として計算)。
Octaveコードで実装するとこんな感じ。
eigenvals = sum(S,1); varianceExplained = sum(eigenvals(1:k))/sum(eigenvals);
以下まとめ。

PCAを圧縮の目的で使用する時
1.svdを共分散行列に対して実行。
2.
\({variance \hspace{3pt} explained = \frac{\sum^k_{i=1}S_{i,i}}{\sum^n_{i=1}S_{i,i}}}\geq 0.99\)
個の式を満たす最小の\(k\)を算出。
以上でデータを何次元まで削減できるかを選ぶことができます。
Advice for Applying PCA
PCAは学習アルゴリズムの実行時間をスピードアップできることについてとPCAを使う際のアドバイスです。
まずは、PCAを学習アルゴリズムの実行時間をスピードアップに使う方法について。
教師あり学習(入力\(x\)とラベル\(y\)があり、\(x^{(i)}\in R^{10000}\))を場面としています。
まず、入力\(x^{(1)}\)から\(x^{(m)}\)のみを取り出します(ラベルなしとなる)。
それにPCAを実行し、削減された次元の表記を取得します(\(z^{(1)}\)から\(z^{(m)}\)\in R^{1000})。そうすると新しいデータセットができます(\(z^{(1)},y^{(1)}\),..,z^{(m)},y^{(m)})。
この新たなデータセットをニューラルネットワークやロジスティック回帰に与えて仮説を学習することができるという流れです。
注意
PCAが実行していることは、\(x\)から\(z\)へのマッピングを定義することであり、トレーニングセットにのみPCAを走らせることを意味しています。クロスバリデーションセットやテストセットに適用してはいけないです。
PCAの応用例まとめ
・データ圧縮
・学習アルゴリズムのスピードアップ(保持される分散の%を調べる)
・可視化(\(K=2,K=3\))
PCAの誤用例
・過学習(オーバーフィット)を防ぐために使用すること
PCAを使用すると、特徴数が\(k\leq n\)と減るとオーバーフィットしにくくなるが、PCAはラベル\(y\)を使用せずに単に入力の\(x^{(i)}\)を使用して低次元の近似値を探します。つまり、PCAはラベル\(y\)の値が何かを知らずに情報を捨てている(次元を削減)ため、重要な情報を捨てる可能性がある。
なので、オーバーフィット防止を目的とするならラベル\(y\)が分かっている正規化を使用するべきです。
・まずはオリジナルの\(x^{(i)}\)のデータで検討する
オリジナルのデータで実施してみて、それがダメなときはPCAを実装して\(z^{(i)}\)を使うことを検討するべき。
さいごに
K-MeansとSVMについて学習しました。
次元削減をすることで容量を減らしたり、学習アルゴリズムのスピードアップを測ることについて理解できました。理論は分かり、一応説明っぽいことはできても実装は難しいですね。初めてなので当たり前と言えばそうなのですが。一つ一つ紐ほどきながら実装していくのは楽しいです。成長している実感がありますね。残りの3week分が終了したら、Pythonで実装してみたいです。
では、引き続き頑張っていきましょう!


