Coursera Machine Learning / week6【学習メモ】

Coursera Machine Learning
Week6【学習メモ】【機械学習】
スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。

機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース（1日1~2時間ペース？）としていますが、気にせずに理解できているか確認しながら進めていこうと思います。

Ⅰ．Advice for Applying Machine Learning

Deciding What to Try Next

機械学習でモデルを作り、結果が大きな誤差を生んだ場合にどうすれば良いかを説明しています。
簡単に言うと、交差検証についてです。

例として、前回使用した家の価格を予想する例を使用し、正則化した線形回帰を実装したとします。学習したパラメータを用いて新しい家の集合の価格を予測した結果、大きな誤差を出してしまったときに学習アルゴリズムを改善するためにはどうすれば良いか？

・より多くのトレーニング手法を使う(トレーニングデータが多い方が良くないこともあり、それは次回説明)
・より少ない数の特徴を使う(オーバーフィッティングを避ける)
・より多くの特徴(データ)を集める(巨大なプロジェクトなどで現在の特徴の集まりは実はそんなに十分な情報を持っていない場合)
・特徴の多項式を追加する
・ラムダや正則化のパラメータを増減する

上記の中からなにを選択すればいいかを分からず、多くの人はランダムに選んでしまい時間を無駄にしてしまう可能性が高いみたいです。それを防ぐためにまず、学習アルゴリズムをどうやって評価するのか学習していきます。

Evaluating a Hypothesis

仮説をどのように評価するのかについてです。
それは、データ全体を通常のトレーニングセットとテストセットに分けることです。一般的には通常のデータセットを70%、テストセットを30%の比率で分けます。ここで、データが順番で並んでいる場合はランダムに70%と30%に分けた方が良いと言っています(既にランダムに並んでいる場合には関係なし)。

・線形回帰
トレーニングセットからパラメータのθを学習して目的関数である、トレーニングの誤差と\(J\)のθを最小化します。
次にテストの誤差を計算します。テストの誤差は\(J_test\)で表します。トレーニングセットで学習したθを\(J_test(\theta)\)に入れて誤差を計算します。以下線形回帰の目的関数。
\(J_{test}(\Theta) = \dfrac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(h_\Theta(x^{(i)}_{test}) – y^{(i)}_{test})^2\)

・分類問題
分類問題の目的関数。以下式(0/1誤判別計量)。
\(err(h_\Theta(x),y) = \begin{matrix} 1 & \mbox{if } h_\Theta(x) \geq 0.5\ and\ y = 0\ or\ h_\Theta(x) < 0.5\ and\ y = 1\newline 0 & \mbox otherwise \end{matrix}\)
\(\text{Test Error} = \dfrac{1}{m_{test}} \sum^{m_{test}}_{i=1} err(h_\Theta(x^{(i)}_{test}), y^{(i)}_{test})\)

これにより、誤分類されたテストデータの割合がわかります。
結果、実はあまり良いモデルではなかったということが多々発生します。よくあるのが、オーバーフィッティング(ハイバリアンス)で、トレーニングデータでは高すぎる精度ではあるが、テストデータだと分類エラーを頻発してしまうことです。ここで、テストセットでも精度を高めるためにモデルを変えようとして、改良されたモデルが出来上がったとします。ですが、そのモデルも結局テストセットに対して精度が高くなるようにできたものであり、新たにデータを入手したときにそのモデルが同様の精度を発揮するかは不明です。そこで、データの分割を2分割ではなく、3分割にするのが次回の話です。

Model Selection and Train/Validation/Test Sets

モデル選択問題について。
モデル選択問題とは、データセットに何次の項まで含めてフィットさせたいか決めたい、つまり学習アルゴリズムに何の特徴を含めるかなどについてです。
そのためには、データセットを訓練(トレーニングセット)、交差検証(クロスバリデーションセット)、テストセットに分ける必要があります。一般的には訓練=60%、交差検証=20%、テスト=20%のデータ量で分けます。
モデル選択の問題に直面した時には、交差検証セットを用いてモデルを選択します。

方法として、ここではまず線形モデル(一次関数)の目的関数を最小化します。すると、線形モデルに対して何らかのパラメータの値\(\theta^{(1)}\)(この1という数字は一次関数の1)が決まります。
同じことを二次のモデルに対して行い、\(\theta^{(2)}\)、さらに10次の多項式モデルまで計算します。
次にこれらのモデルを交差検証セットで評価します。
\(J_{cv}(\Theta(1))\)
仮説が交差検証セットに対して良く機能するかを評価し、最小の交差検証セットでの誤差のモデルを選びます(ここでは4次の多項式をモデルとして使用)。パラメータ\(d\)は多項式の次数なので、ここでは\(d=4\)になります。
ここで、選んだモデルをテストセットで使用することで、一般化エラーを推定することができます。
\(J_test(\theta(4))\)

仮説のモデルを選択するために、各次数の多項式をテストし、エラー結果を確認することができるわけですね。

バイアスとバリアンス

バイアスとバリアンスについて。
学習したアルゴリズムを走らせて、あまりいい結果が出なければそれはアンダーフィット問題かオーバーフィット問題かのどちらかです。どっちが問題になっているかを見分け、それを元にどう改良すればよいかを考えることが大切というわけですね、
アンダーフィットとオーバーフィットについてはweek3のメモで調べました。
Coursera Machine Learning / week3【学習メモ】

バイアスとバリアンス(分散)、どちらが悪い予測の問題となっているかの予測をします。
以下参考図です。(coursera machine-learningより)

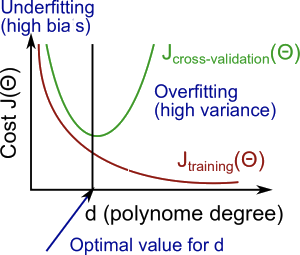
多項式の次数d(横軸)を増やすと、トレーニングエラーは減少する傾向があります。

同時に、交差検定誤差は、dをある点まで増加させると減少する傾向があり、dが増加すると増加し、凸曲線を形成します。

ハイバイアス(アンダーフィッティング)とは、\(J_{train}(\Theta)\)と\(J_{cv}(\Theta)\)が共に高く、\(J_{train}(\Theta)\approx J_{cv}(\Theta)\)の状態です。

ハイバリアンス(オーバーフィッティング)とは、\(J_{train}(\Theta)\)が低く、\(J_{cv}(\Theta)\)は\(J_{train}(\Theta)\)よりはるかに高くなります。

Regularization and Bias/Variance

正則化のバリアンスとバイアスについて。
以下図参照。

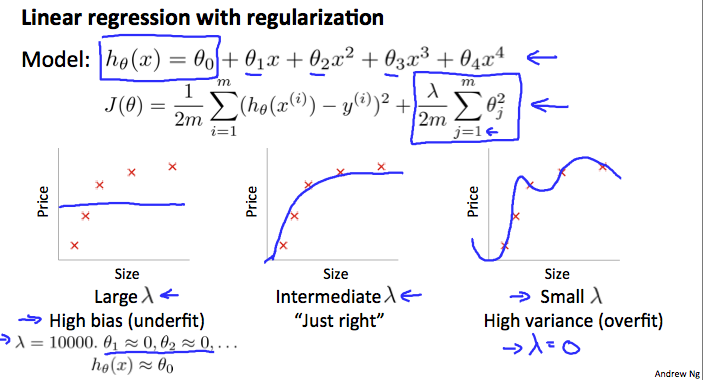
上記の図では、\(\lambda\)が大きいと並行線のようになってしまい、フィットが固くなっています(ハイバイアス/アンダーフィット)。逆に\(\lambda\)が小さすぎるとデータが過剰適合していますね(ハイバリアンス/オーバーフィット)。

では適切なモデルと\(\lambda\)を選択するにはどうすれば良いか、以下のステップを踏みます。

1.\(\lambda\)のリストを作成。(例:0.01→0.02→0.04→0.08→0.16→…→10.24)
2.異なる次数のモデルを作成。
3.全モデルに対して\(\lambda\)を試し、最適な\(\theta\)を学習する。
4.学習したパラメータ\(\theta\)と\(\lambda\)をを使って、交差検証誤差を計算。
5.交差検証誤差が最も低くなっった組み合わせを選択。
6.テストセットに対しての誤差を計算し、未知のデータに対応できるかを確認。

以下\(\lambda\)と\(J(\theta)\)のグラフ図です。

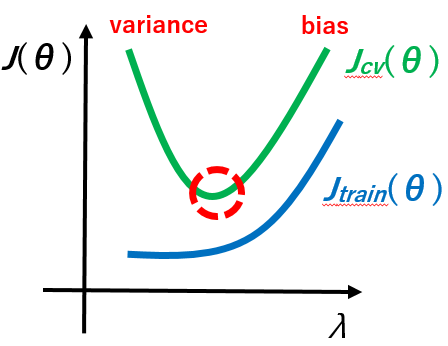
\(\lambda\)が小さすぎると、モデルはオーバーフィット(ハイバリアンス)になるのでトレーニングセットのエラーは小さく、交差検証セットのエラーは大きくなります。

\(\lambda\)が大きすぎると、モデルはアンダーフィット(ハイバイアス)になるのでトレーニングセットのエラーは大きく、交差検証セットのエラーは大きくなります。

Learning Curves

データ数と誤差の学習曲線(Learning Curves)についてです。
横軸がm(トレーニングセットの数)で縦軸が誤差数です。

ハイバイアス(過小学習)のとき

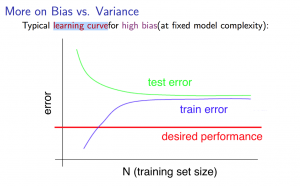
トレーニングセットの数が少ないと、\(J_{train}(\Theta)\)の誤差は低くなり、\(J_{cv}(\Theta)\)の誤差は高くなります。
ハイバイアスの特徴として、トレーニングセットの数が増加していくと、\(J_{train}(\Theta)\)と\(J_{cv}(\Theta)\)の誤差は共に高くなり、近似値となります\(J_{train}(\Theta)\approx J_{cv}(\Theta)\)。過小学習のためうまくデータにフィットせず、パラメータの数が少ない上にデータの数はたくさんあるという状態のためですね。
そして、トレーニングセットの数が増加し続けたとしても(グラフが右に続いたとしても)、\(J_{train}(\Theta)\)と\(J_{cv}(\Theta)\)の誤差は近似値のままほぼ変わらないため、学習アルゴリズムがハイバイアスが原因で上手くいかないときはトレーニングセットのデータ数を多く取得しようとしても解決にはなりません。なぜなら、最終的には\(J_{cv}(\Theta)\)か\(J_{test}(\Theta)\)の誤差を最小化したいわけなので、さらにトレーニングデータの数を取得したとしても\(J_{cv}(\Theta)\)の誤差は大して下がらないからです。

ハイバリアンス(過学習)のとき

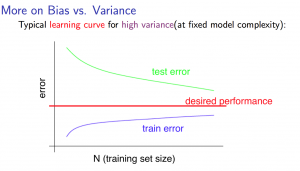
トレーニングセットの数が少ないと、\(J_{train}(\Theta)\)の誤差は低くなり、\(J_{cv}(\Theta)\)の誤差は高くなります。
トレーニングセットの数が増加していくと、\(J_{train}(\Theta)\)の誤差は徐々に高くなっていきますが、\(J_{cv}(\Theta)\)の誤差は横ばいにならず徐々に減少していきます。
ハイバイアスが起こっているときの特徴として、トレーニングセットの数が増加した時、誤差が\(J_{train}(\Theta)<\(J_{cv}(\Theta)\)となります。
そして、最終的には\(J_{cv}(\Theta)\)か\(J_{test}(\Theta)\)の誤差を最小化したいわけなので、ハイバイアスのときにはトレーニングデータの数をさらに取得していけば、\(J_{cv}(\Theta)\)の誤差は減少してくため、ハイバイアスで上手くいかないときにはトレーニングデータの数をさらに取得することは解決につながるということになります。

Deciding What to Do Next Revisited

week6の初めに学習したハイバイアスとハイバリアンスのときに改善するための6つの手段について話しています。

データ数を増やす	ハイバイアス(過小学習)
特徴量を減らす	ハイバリアンス(過学習)
特徴量を増やす	ハイバイアス(過小学習)
多項変数を増やす\(x^{1},x^{2},x^{2}_1,x^{3}_2\)など	ハイバイアス(過小学習)
\(\lambda\)の値を減らす	ハイバイアス(過小学習)
\(\lambda\)の値を増やす	ハイバリアンス(過学習)

パラメータが少ないニューラルネットワークは、適合しにくい傾向があります(過小学習)。また、計算コストも安くなります。
より多くのパラメーターを持つ大規模なニューラルネットワークは、過剰適合しがちです(過学習)。また、計算コストも高くなります。この場合、正則化（\(\lambda\)を増やす）を使用して過剰適合に対処できます。

デフォルトでは、隠れ層は1つです(1つから始めていくのが推奨)。

Ⅱ．Machine Learning System Design

Prioritizing What to Work On

機械学習のシステムを使った例として、スパムメールの分類について説明しています。
スパムメールを分類する機械学習アルゴリズムの例を説明しており、高い正確性と低いエラーにするためにはどうすればよいか？
・もっと多くのデータを集める。(はちみつ壺プロジェクトと呼ばれる偽のe-mailアドレスを使って、それをスパマーにつかませ、大量のスパムメールを集める方法)
・さらに洗練された特徴を開発する。(e-mailのヘッダを見て、ルーティング情報をうまくとらえるような洗練された特徴を開発して、それがスパムかどうかを判定する)
・e-mailのテキストを見て、もっと洗練された特徴を構築する。(discountsとdiscountを同じ単語と見なすか、記号について複雑な特徴にするか)
・故意のスペルミスを検出するためのアルゴリズムを開発する。

4つの方法を挙げたが、どれに時間をかければ良いかというのは決まっていないらしい(どれが一番良い方法かを選ぶのは難しい)。次回講義で詳しく説明。
スパムを含まれている単語で分類する時の方法。ベクトルで0/1で表している。

Error Analysis

エラー分析について。
1.機械学習の課題に対して、はじめに複雑で多くの特徴を持つようなシステム構築から始めるのではなく、シンプルなアルゴリズムで手早く実装できるものから始めた方が良いみたいです(早くて汚い実装)。そしてそれをクロスバリデーションでテストします。
2.その後、トレーニングとテストの誤差の学習曲線をプロットし高バイアスか高バリアンスかそれ以外化を見分ける。そして、より多くのデータや特徴が必要か考える。
3.学習アルゴリズムがエラーになったものを手動で確認し、何らかのパターンやアルゴリズムにとってもっとも分類が困難なものは何かを判断する。

discount/discounts/discountingなどの単語を同一として扱いたいとしたときに、例として単語の初めの数文字を見る方法がある。ここでいうなら初めのdiscountという単語が3つとも含まれている。これを識別するには自然言語処理をする必要があり、ステミングソフトウェア(語幹を取り出すソフトウェア)を使用するとよい(porter stemmerが良いみたい)。

ステミングありとなしでクロスバリデーション誤差を見ることで有意な差が見られるなら、使用するべき。このときの単一実数による評価指標として、クロスバリデーションの誤差で判断しているということができる(今回は簡単例)。

Error Metrics for Skewed Classes

エラーのメトクリスとは、学習アルゴリズムがどれだけうまくやっているかがわかる単一の実数値による評価指標のことでした。評価とエラーのメトクリスにおいて、学習アルゴリズムに対して適切なエラーの指標、適切な評価の指標を得るのがトリッキーになるケースがある。そのケースはスキューした(歪んだ)クラスと言われるものです。このことについて説明されています。

例として、ロジスティック回帰を使用してテストした時に1%のエラーが出たとします。言い換えると99%の精度です。しかし、トレーニングセットとテストセットの0.5%しかがん患者がいなかったとすると、99.5%は非がん患者ということになります。そこで、がんの陽性・陰性を分類する場合、がんの陰性データが全体の99.5%、すべてを陰性と予測すればそれだけで正答率が99.5%になってしまいます。未学習データ(y=0と予測するだけのもの)ともなりえますね。

スキューしたクラスに直面した場合、別のエラー指標と評価指標を使用します。
その一つに適合率と再現率というものがあります。

分類問題でのモデルの予測は以下の図でまとめることができます。

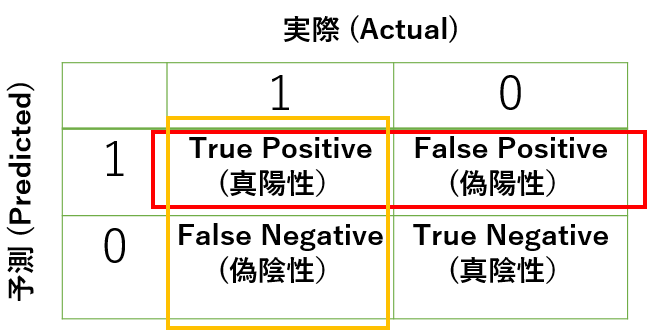
このとき、適合率(Precision)、再現率(Recall)を以下のように定義します。

\(Precision = \frac{True Positive}{True Positive + False Positive}\)
\(Recall = \frac{True Positive}{True Positive + False Negative}\)

適合率(Precision)は、\(y=1\)だと予測したうち、実際に\(y=1\)な割合で、真陽性の数を、赤で囲まれた数(\(y=1\)と予測した値)で割ると求めることができます。

再現率(Recall)は、実際に\(y=1\)である数のうち、正しく\(y=1\)であると予測できた割合で、真陽性の数を、橙色で囲まれた数(実際に\(y=1\))で割ると求めることができます。

さきほどの\(y=0\)と予測するだけ未学習データは再現率が0になります。\(y=1\)と予測するデータがないわけですからね。
適合率と再現率は高いほど有効だと言われています。

Trading Off Precision and Recall

適合率(Precision)と再現率(Recall)の関係性について。
適合率と再現率はトレードオフの関係で一方を高くするともう一方が低くなります。また、両者を統合した指標は、F値という調和平均(相加平均ではない)を使います。
\(2\frac{Precision×Recall}{Precision+Recall}\)
モデルの予測値\(h\theta(x) \)がある閾値より大きい時\(y=1\)だと予測すると、閾値が小さければ再現率は上がり適合率は下がる、逆に大きければ適合率が上がり再現率が下がります。
適合率と再現率をバランスよく定量化したものが上記のF値です。
アルゴリズムが複数あるとき、F値が高いものを選択すると偏りがなくなるでしょう。

Data For Machine Learning

機械学習において、どれだけのデータを使用すればよいかについて説明されています。

特徴\(x\)に\(y\)を正確に予測するのに必要な情報が含まれている場合、大量のデータを集めることは精度向上に役立ちます。特徴\(x\)が\(y\)を予測するのに必要な情報が含まれていないときには大量のデータを集めても時間の無駄になるということですね(家のサイズだけしか情報ないのにさらに家のサイズだけの情報を大量に集めても家の価格の予測の精度は向上しないよねって話)。

Ⅲ．さいごに

week6が無事終了しました。今回の内容は計算要素は少なく、つくったモデルの評価の仕方について学習しました。評価に際してどう改善すればよいかも学習できたと思います。内容は地味でしたが、感じとしてはかなり重要なんじゃないかなと思います。特に評価と改良については知らないとどうすればいいか分からずに時間を浪費してしまう可能性が高いと思われるため。

次回はweek7ですね。引き続き頑張っていきましょう！