Coursera Machine Learning
Week10【学習メモ】【機械学習】
スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。
機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース(1日1~2時間ペース?)としていますが、気にせずに理解できているか確認しながら進めていこうと思います。
今回はビッグデータを扱うのでワクワクしています(*’ω’*)
Ⅰ.Large Scale Machine Learning
Learning With Large Datasets
「機械学習においては、最も良いアルゴリズムを持つ者でなく、もっともデータを持っている人だ」という名言があります。
ただ、大量のデータを集めることが本当に意味のあることなのかを判断する必要があります(week6参照)。それが以前学習したハイバイアスとハイバリアンスの関係です。ハイバイアスの状態だと、誤差が大きくてもデータを増やすことは解決にはつながりません。逆に、ハイバリアンスの状態だと、誤差が大きい場合、データ数を増やすことは解決につながります。
Stochastic Gradient Descent
確率的最急降下法のついてです。
week1で学習した最急降下法は別名バッチ最急降下法とも呼びます。
以下の式で算出していました。
\(\theta_j := \theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(({h}_\theta(x_i) – y_i)x_{j})\)
「バッチ」とは、一度にすべてのトレーニング手本を見ることを意味しています。
例として、\(m=30000000000\)という膨大なデータ数があったとします。このアルゴリズムとして、全てのデータを1回で読み込み処理しなくてはなりません。そうしてようやく、最急降下法での1ステップを進めることができます。これを最小になるまで繰り返すわけですから、CPUには大きな負荷がかかります。
以下確率的最急降下法のステップです。
1.データセットをランダムにシャッフルする。つまり、\(m\)個のトレーニング手本をランダムに並べ替えることです。
2.以下の式で1回の計算につき1つのデータのみを使用します。
\((for \hspace{4pt} i = 1, …, m )\)
\(\theta_j := \theta_j – \alpha (h_\theta(x^{(i)}) – y^{(i)})x_j^{(i)}\hspace{10pt} (for \hspace{4pt} j = 0, …, n)\)
つまり、各データ毎のアップデータを総データ数\(m\)回繰り返すことで目的関数\(J\theta\)を最小にするパラメータ\(\theta\)を見つけようということです。
また、1番目にランダムにシャッフルをするのは、ソートされた順番で計算すると偏りが発生してしまうためです。
ただし、バッチ最急降下法は繰り返し計算するごとに目的関数\(J\theta\)は小さくなっていきますが、確率的最急降下法は必ずしも小さくなっていくとは限りません。むしろ遠回りします。これは、1つのデータのみを最適化するため間違った方向に進む可能性があるからです。
他にも、バッチ最急降下法は大域的最適解(global optima)に収束しますが、確率的最急降下法は(global optima)には収束せずに、その周りをさまようことになります。しかし、同じように収束はしなくても近似値にはなるので、そこまで仮説として使用しても気にする必要はありません。
確率的最急降下法は、1データに対する学習を複数回(1から10回程度)行います。ただ、データ\(m\)が大量にある場合は1回でも十分です。データ数に依存して1データに対する学習回数を判断します。
Mini-Batch Gradient Descent
ミニバッチ最急降下法(Mini-Batch Gradient Descent)についてです。
一度以前までの手法を整理しておくと、バッチ最急降下法は一度にすべてのデータ\(m\)の処理をしていました。確率的最急降下法は一度に一つのデータのみを処理していました。
ミニバッチ最急降下法はその二つの手法の間に位置しており、\(b\)このデータを処理します(\(b\)のことをミニバッチと呼ぶ)。\(b\)の数値の選択としては10が多く、選択する範囲としては2-100が多いです。
例を以下図で説明しています。

上記の図では、10個のデータを100回に分けて計算しています。なので、\(i+9\)となっており、forループは\(1,11,21,…,991\)となっています。
では、確率的最急降下法とミニバッチ最急降下法はなぜ使い分けられるか?
それは良いベクトル化実装があるときだけです。10個の手本に渡る和は、よりベクトル化した形で実行でき、その方が計算において部分的に並列化しやすいからです。言い換えると、微分項を計算するために適切なベクトル化実装を使えば、数値計算代数ライブラリを使うことができ、\(b\)手本に渡る微分の計算を並列化できます。
逆にミニバッチ最急降下法のデメリットとして、新たなパラメータ\(b\)を使用するため、その設定に時間を浪費してしまう可能性があります。ただ、ベクトル化した実装によっては確率的最急降下法よりも早く処理することができます。
Stochastic Gradient Descent Convergence
確率的最急降下法が正しく収束しているかを確認と学習率\(a\)を選ぶ方法についてです。
確率的最急降下法のコスト関数は以下で計算します。
\(cost(\theta, (x^{(i)}, y^{(i)}))=\frac{1}{2}(h_\theta(x^{(i)}-y^{(i)})^2)\)
単体のトレーニング手本に関するパラメータ\(\theta\)でのコストは、単にそのトレーニング手本における二乗誤差の半分です。
確率的最急降下法が収束しているかを確認する方法は、未学習の次の1件のデータを計算する前(パラメータを更新する前)にそのトレーニング手本に対し、仮説がどれだけ良いかを計算するものです。
他にも、1000回繰り返したときに、次のデータを計算する前にコストをの平均の値をプロットするというものがある。1000回ではなく、5000回の平均をプロットすると、1000回のときよりもグラフが滑らかになるが、欠点として、5000回という計算をしたにもかかわらず、プロットできるグラフは1つのみになってしまい、アルゴリズムがどれだけよく動いているかをフィードバックするのが遅くなってしまう。
以下プロット図です。
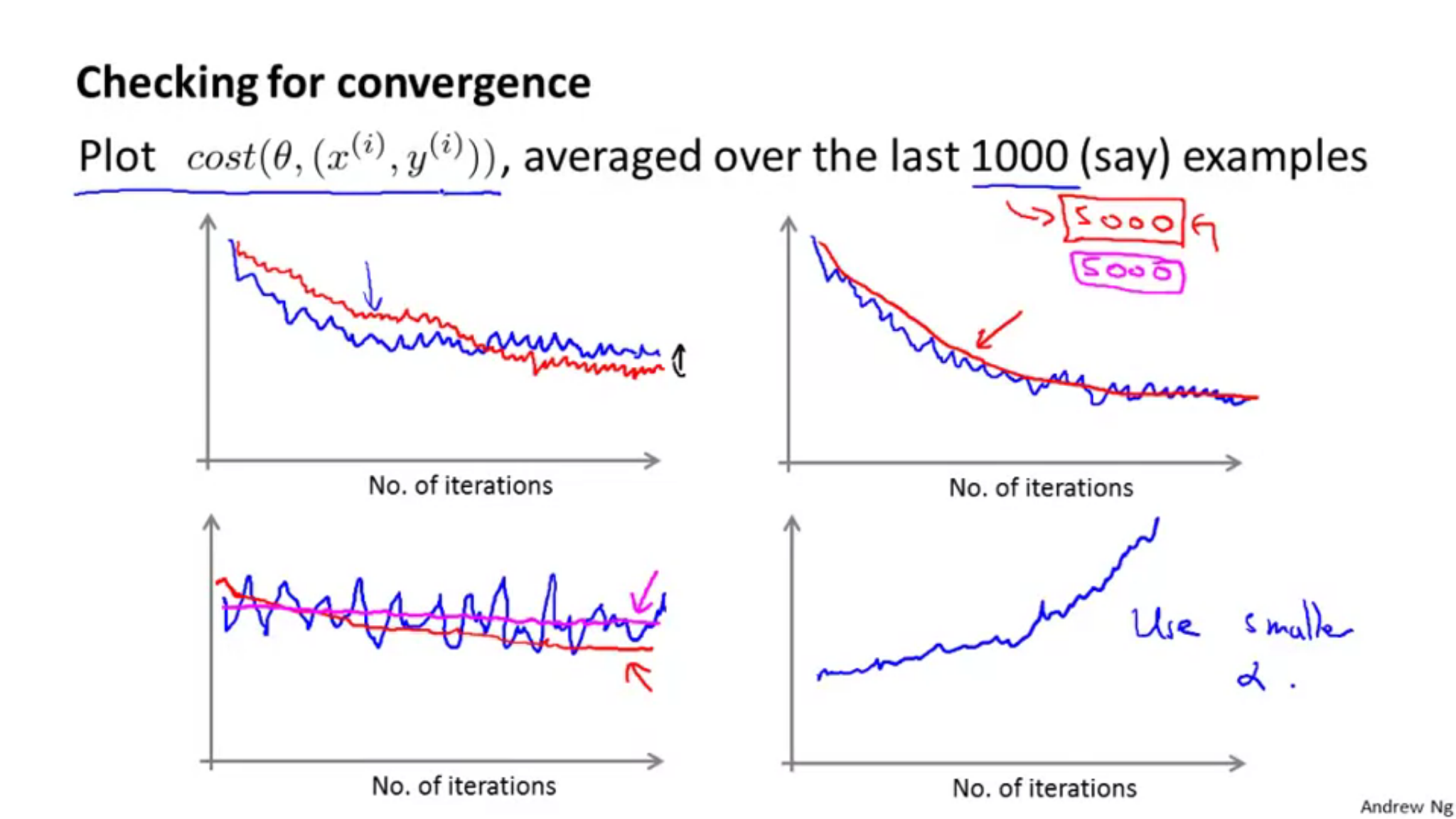
青いプロット線が1000回の平均で、赤いプロット線が5000回の平均です。
1000回の平均のグラフが荒れている場合には、平均回数を増やしてあげると滑らかなグラフになります。
上の二つのグラフは収束しているように見えるので大丈夫ですが、下左のグラフはうまくアルゴリズムが学習できていないせいか並行になっています。そのときには学習率や特徴を変える必要があります。下右のグラフでは、誤差が増加してしまっている(アルゴリズムが発散している)ときには、より小さな学習率\(a\)を使用すると改善されます。
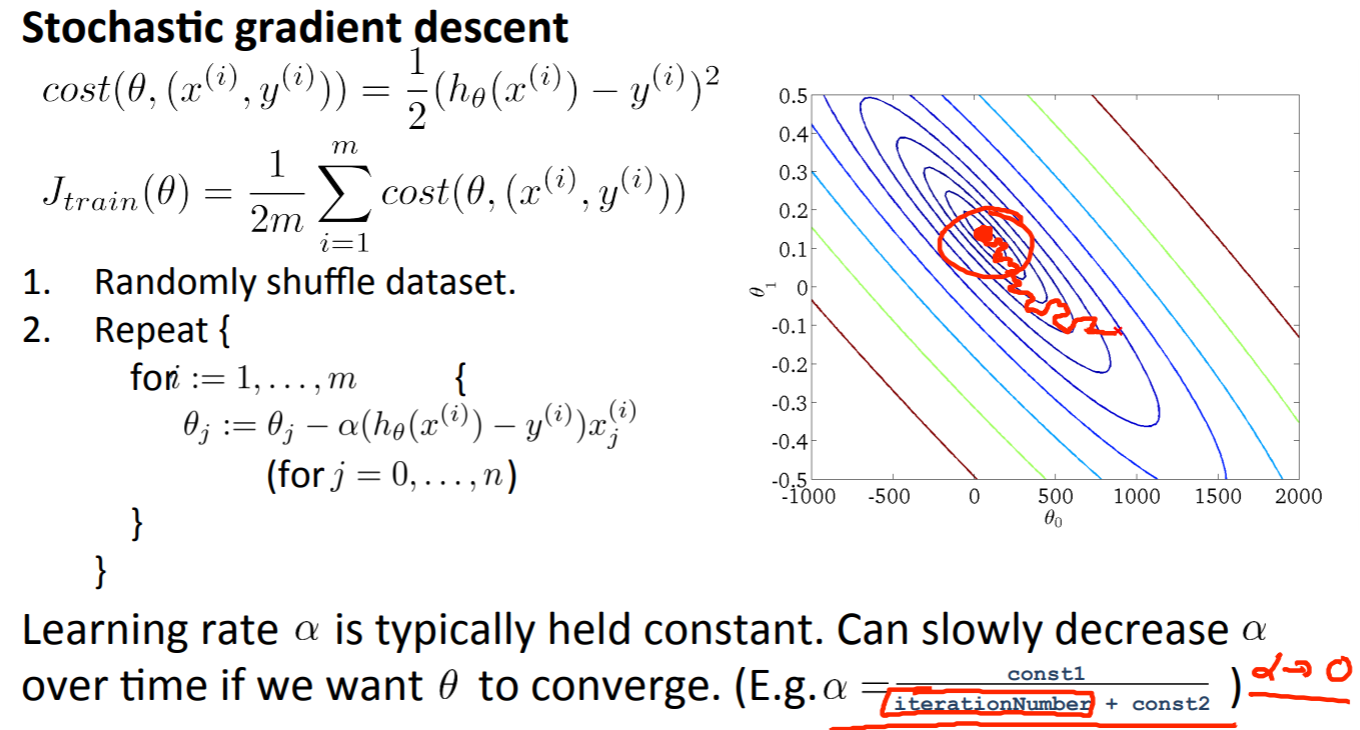
次に学習率\(a\)についてですが、一般的な確率的最急降下法の実装では学習率\(a\)は定数のまま据え置くのが普通です。もし、収束させたいなら学習率\(a\)を徐々に小さくしていくと収束します。
そのときの学習率\(a\)の求め方が以下の式です。
\(\alpha = \frac{constant 1}{iterationNumber + constant 2}\)
この式はアルゴリズムを走らせるほど、イテレーション回数(リピート回数)が大きくなっていくので学習率\(a\)はゆっくりと小さくなっていき、最小に収束するまで小さくなります。ただし、二つのパラメータが登場するので、それを定義するのに時間がかかってしまうのが欠点です。
Online Learning
オンライン学習についてです。名目が興味を引きますね。
ネットショッピングを例にすると、ユーザーが行き来しつつ様々な行動をとります。そのときに、ユーザーの行動や嗜好を予測させて、モデルがオンラインで学習することができれば、ユーザーに合った商品や値段を提示することができ、購入確率が高くなり、利益につながりますね。
ユーザーの行動や価格などの情報\(x\)とパラメータ\(\theta\)を使用して、ユーザがある行動(クリックや購入)をする確率は以下のように算出できます。
\(p(y=1 | x; \theta)\)
使用するデータを\(x^{(i)},y^{(i)}\)と表記せずに、\(x,y\)と表記するのは、一度使用したデータは捨て去り、計算するときの1度のみ使用するため、わざわざインデックスをつけなくても大丈夫というわけです。このときに使用するデータは1つのみです(1度の計算に必要なデータは1つのみ)。
Map Reduce and Data Parallelism
MapReduceと並列化についてです。
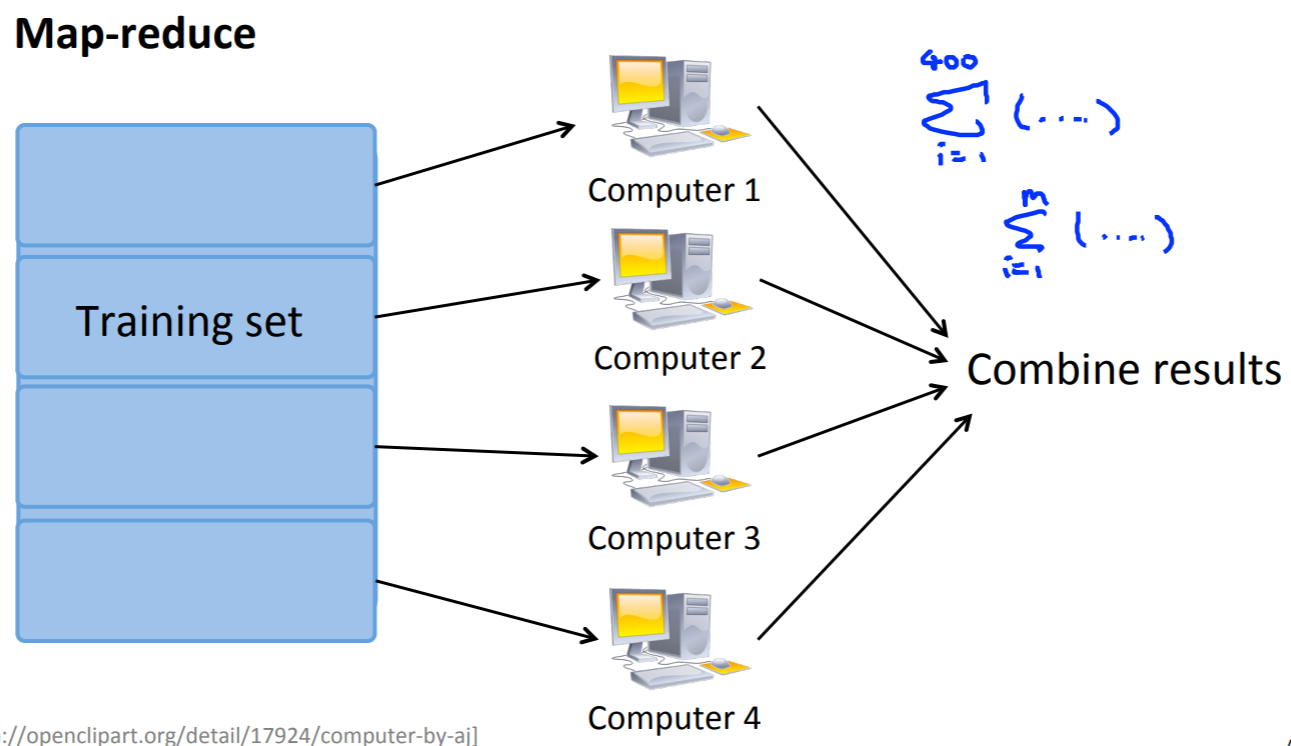
今までの機械学習の計算処理は1つのマシンの使用を想定してきましたが、時には単純にデータがあまりにも大きいために、1つのマシンでは処理しきれないこともあります。
そこで、大規模機械学習において、異なるアプローチであるMapReduceと呼ばれるものを使用していきます。
以下参考図です。
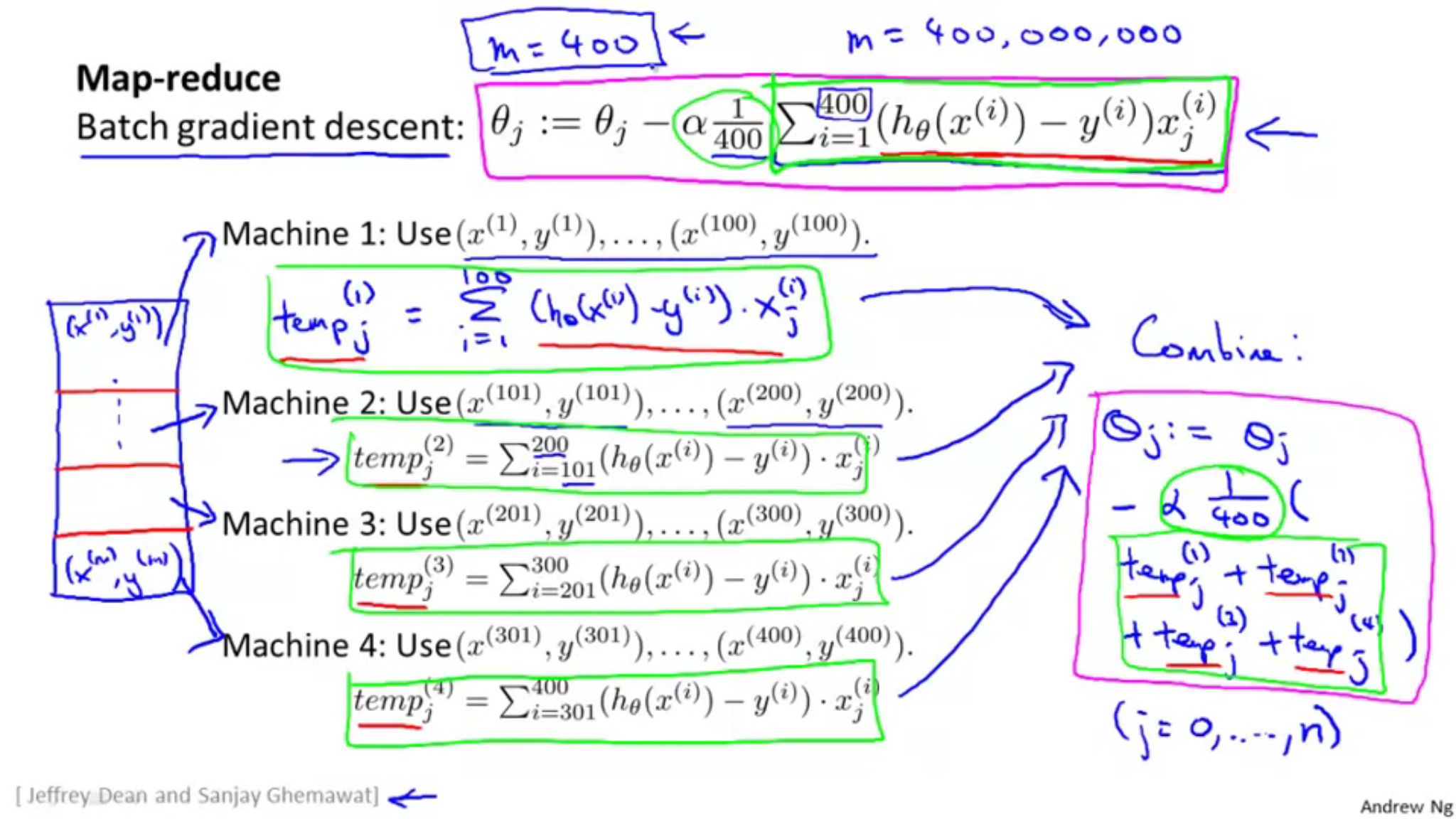
\(m=400\)のデータを4分割して処理を分けています。それぞれの計算が終わった後に、1つにまとめ上げて結果を算出するという手順です。
さいごに
今回は計算がほどんどない講義でしたので、3時間前後で終了しました。
ビックデータ解析、大規模な機械学習についてのお話しでした。
あまり具体的な部分には触れませんでしたが、ざっくりとした内容は把握することができました。
次回でmachine-learning講義も終わりですが、楽しんで学んでいきたいと思います。


