Coursera Machine Learning / week9【学習メモ】

Coursera Machine Learning
Week9【学習メモ】【機械学習】
スタンフォード大学のAndrew Ng氏が手掛ける機械学習講義の学習メモ。

機械学習のスキルと知識を付けるために2020/10/30からスタート。全講義を終えるのに11週間をベース（1日1~2時間ペース？）としていますが、気にせずに理解できているか確認しながら進めていこうと思います。

week9が見たところ一番時間がかかりそうなので、じっくりと学習していきたいと思います！

Ⅰ．Anomaly Detection

Problem Motivation

異常検知(Anomaly Detection)について説明しています。
異常検知は教師なし学習でありつつ、教師あり学習とも似ている点があります。
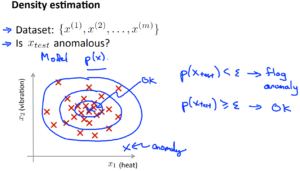
飛行機のエンジンを例として、以下の2つの特徴量を持ちます。

\(x_1\):エンジンから生成される熱量
\(x_2\):振動
データセット:\(x^{(1)}\)~\(x^{(m)}\)まで所持
\(x_{test}\):新たな航空機のエンジン(これが異常かどうか調べたい)

上記のグラフの説明としては、データセットをプロットしたものが×で記されています。
新たな航空機エンジンを緑色の×で表しています。このときに、緑色のエンジンがデータセットの集合体の近くにプロットされれば問題なしとなりますが、離れた場所にある場合は異常検知となります。

ではどのようにして、異常検知かそうでないかを判断するのでしょうか？

まず、\(x^{(1)}\)~\(x^{(m)}\)までのデータセットを異常検知ではないと想定します。
ラベルなしのトレーニングセットが与えられた時に、モデル\(p(x)\)を構築します(xのときの確率モデル)。
そのモデルを使用して、\(p(x_{test})\)が閾値\(\epsilon\)(イプシロン)より小さいかを見ます。

\(p(x_{test})<\epsilon\)なら異常
\(p(x_{test})\geq \epsilon\)なら正常

異常検知の応用例としては、webサイトで怪しい動きをしているユーザーを検知して、何らかの対処をすることができます。他にもデータセンターのコンピュータをモニタリングすることにも使われています。

Gaussian Distribution

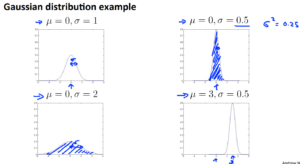
ガウス分布(Gaussian Distribution)について。
ガウス分布とは正規分布(確立関数の式とも言う)の事です。以下の式で算出できます。

\({p(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)
}\)

平均\(\mu\)と分散\(\sigma^{2}\)の値をパラメータとしてとり、計算します。

Algorithm

異常検出のアルゴリズムについてです。

１．特徴を選ぶまたは見つける
異常検出となるサンプルとしての特徴を探します。システムに悪意のあるユーザーがいるような大きく外れた値を持つサンプルを選びます。いわゆるラベルを持たないデータセットを用意するということでしょうか。

{\(x^{(1)},…,x^{(m)}\)}

２．平均値を算出する
平均値\(\mu_j\)を算出します。

\({{\mu_j = \frac{1}{m} \sum^m_{i=1}x_j^{(i)}}
}\)

３．分散を算出する
分散(標準偏差)\(\sigma^{2}_j\)を算出します。

\({{\sigma_j^2 = \frac{1}{m} \sum^m_{i=1} (x_j^{(i)} – \mu_j)^2}
}\)

４．異常値の可能性がある新たなデータ\(x_test\)を使用し、\p(x_{test})\)を計算する

\(p(x_{test}) = \Pi^{n}_{j=1} p(x_j; \mu_j, \sigma^2_j) = \Pi^n_{j=1} \frac{1}{\sqrt{2\pi} \sigma_j} exp(-\frac{(x_j – \mu_j)^2}{2\sigma_j^2})\)

\(p(x) < \epsilon\)なら異常と判断します。

つまり、正規分布から外れているものを外れ値とするわけですね。

上記の式はガウス確率の式でもあります。

Developing and Evaluating an Anomaly Detection System

異常検知システムの開発と評価についてです。

・\(y=0\)を正常、\(y=1\)を異常とする。
・ラベル付けされていないトレーニングセット(基本正常なデータの集まりだが、少し異常なデータが紛れ込むくらいならok)
・交差検証とテストセットを定義し、個々の異常検出のアルゴリズムの評価を行う(どちらも異常なサンプルが含まれている前提)。

例として、10000個の正常な部品と20個の異常な部品があったとします。
その10000個のデータを訓練=60%(ラベルなし(\(y=0\)に対応))\(p(x)\)に適用するために使用(\(\mu_n,\sigma^{2}_n\)まで続くほぞ正常なデータ)、交差検証=20%、テスト=20%のデータ量で分けます。
20個の異常な部品は、交差検証とテストに50%ずつ振り分けます。
例の部品を振り分けると、正常な6000個は訓練・正常な2000個と異常な10個は交差検証(ラベル付けけあり)・正常な2000個と異常な10個はテストに振り分けられます(ラベル付けあり)。

・まず、トレーニングセットを使用してモデル\(p(x)\)を作成します(ラベル付けされていないが、正常なものと想定)。
・その後、交差検証セットとテストセットを使用して
\(y = 1 \hspace{15pt} if \hspace{15pt} p(x) < \mu \hspace{15pt} (anomaly)\)

\(y = 0 \hspace{15pt} if \hspace{15pt} p(x) \ge \mu \hspace{15pt} (normal)\)
と分類する。

では、どのようにアルゴリズムを評価すればよいか？

上記の分類精度\(y=0\)と\(y=1\)だと、偏りがある(正常データのほうが圧倒的に多い)ため、評価指標にはなり得ない。
なので、その代わりに以前学習したF値を使います。
Coursera Machine Learning / week6【学習メモ】

最後に\(\sigma\)をどのように決めるかですが、これは交差検証で評価時にF値を見ながら最適な数値を決めていきます。

Anomaly Detection vs. Supervised Learning

前回、異常検知でラベル付きのデータを使用しましたが、それじゃ教師あり学習はなぜ使わないのか？という疑問が出てきます。今回はどのときに教師あり学習・教師あり学習を使用するべきなのかを説明しています。

・もし陽性/異常\(y=1\)のサンプル数がとても少ない(0-20くらい)場合は異常検知を使用した方が良いです。数少ない陽性のサンプルを交差検証セットとテストセットに使用した方が良い。
・上の状況とは相対的に、陰性/正常\(y=0\)のサンプル数が大量にある場合も異常検知の使用を検討した方が良いです。\(p(x)\)を推計する時には陰性のサンプルのみ必要となるため、陰性のデータが大量にある場合には、\(p(x)\)を作成するのが良い。
・異常検出を適用するときには、多くの異なる種類の異常が検出されます。さらに、陽性のサンプル数が少ないと、十分なアルゴリズムを学習するのは難しく、新たな異常を検出する可能性もある。その場合は、単純に陰性のサンプルをガウス分布のモデル\(p(x)\)でモデリングする方が良い。

・陽性と陰性のサンプル数がどちらとも大量にある場合は、教師あり学習を検討するべきです。
・陽性のサンプル数をそこそこ持っているなら、アルゴリズムを学習させられそうで陽性について分かりようであり、将来的に似たような陽性のサンプルが出現しそうなら、教師あり学習のアルゴリズムの方が合理的である。

スパムメールが教師あり学習を使用しているのは、陽性データであるスパムメールを大量に持っているからである。

Choosing What Features to Use

どの特徴をどれだけ使うかを説明しています。

異常検出のアルゴリズムにデータを与える前に、そのデータのヒストグラムをグラフにプロットしてみて、正規分布に近い形になっているかを確認しています(正規分布になっていなくてもok)。
プロットしたグラフの形が非対称(正規分布とは程遠い)だと、様々なデータ変換を試してもっと正規分布に見えるようにします。具体的には\(log(x)\)関数やルート(実際には1/2や0.05などになる)を使用して\(x\)の値を調整し、ヒストグラムを確認しながら正規分布に近くなるよう変換を行います。

次に異常検出に使用する特徴をどう見つけるかについてです。
誤差分析の手順。アルゴリズムがフラグ付けに失敗した異常値を直接調べて、何か普通ではないところを探し、それを用いて新しい特徴をつくる。他にも、既にある特徴を利用し、関係がありそうな特徴同士で割ったものを新たな特徴にするとかでも良い。

Multivariate Gaussian Distribution

多変量ガウス分布(Multivariate Gaussian Distribution)について。
前回学習した通常のガウス分布では対応できない場合があります。それは下図の左のような分布を持ったデータです。特徴量\(x1,x2\)が関連していて中心から同心円状に分布しないような場合です。

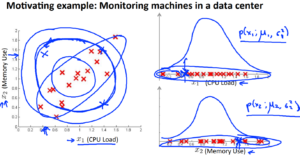
一見左の図では、正常なサンプルとはかけ離れた場所に×がありますが、右の2つの図で見てみると、正規分布のやや端っこではありますがそれほど異常な値とは言えないデータと判断できます。そのため、左の図を元にすると誤って異常と判断されてしまいますね。

そこで、多変量ガウス分布(多変量正規分布)を使用します。
\(p(x_1)\)\(p(x_2)\)と別々にする代わりに、\(p(x)\)と全部を一度にモデリングします。そして、ここではパラメータ\(\mu\)と\(\Sigma\)(n×nの共分散行列)を使用します(svcで使用したもので和ではない？)。今回は\(\Sigma\)は\(|\Sigma|\)として計算するので、Octaveでは以下のように実装します。

以下分布図です。

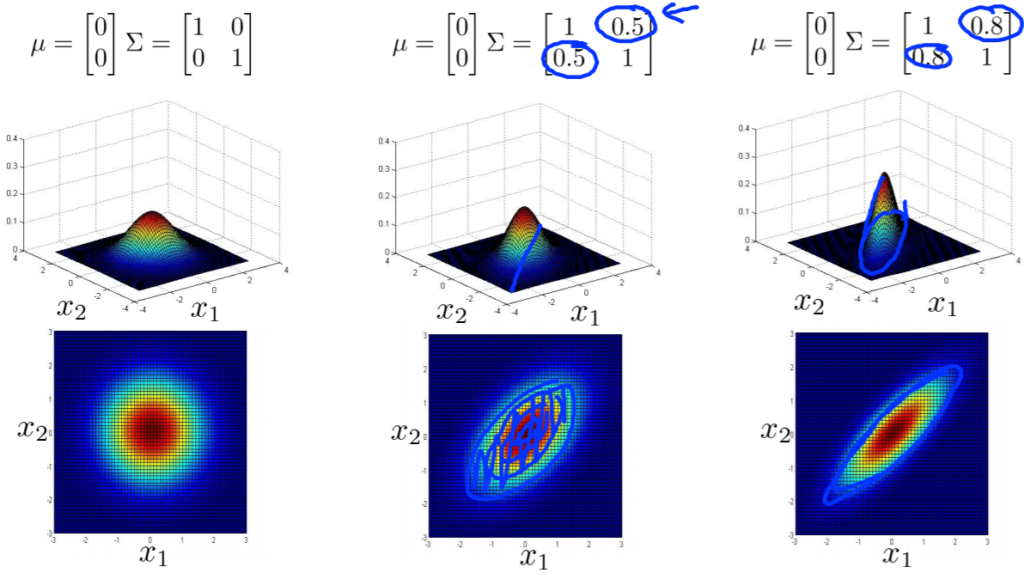
\(\Sigma\)の二つの値が大きくなるとグラフの高さが小さくなり、幅が広がります。値が小さくなるとグラフの高さが高くなり、幅は狭まります。
\(\Sigma\)の一方の値のみを変更すると、特徴\(x_1\)の分散が小さくなり\(x_2\)は同じ値を保った場合は横の長さが短いグラフができ、特徴\(x_1\)の分散が大きくなり\(x_2\は同じ値だと横長のグラフができる。

もし\(\Sigma\)に負の値を入れてみると正の相関(右斜めのグラフ)から負の相関(左斜めのグラフ)になります。また、\(\mu\)の値を変えるとピーク値または中心(コブの部分)が移動します。

Anomaly Detection using the Multivariate Gaussian Distribution

多変量ガウス分布を使った異常検知について説明しています。
以下の計算をして異常かどうかを判断します。

まず、{\(x^{(1)},x^{(2)},…,x^{(m)}\)}のデータセットがあります。

1.平均値\(\mu_j\)を算出します。

\(\mu_j = \frac{1}{m} \sum^m_{i=1}x_j^{(i)}\)

2.共分散行列\(\Sigma\)を求めます。

\(\Sigma = \frac{1}{m} \sum^m_{i=1} (x^{(i)} – \mu) (x^{(i)} – \mu)^T\)

3.多変量ガウス分布の式にて\(p(x)\)を求め、閾値\(\epsilon\)と比較し、移乗か判断する。

\({p(x) = \frac{1}{\frac{1}{(2\pi)}^{\frac{n}{2}} | \Sigma |^{\frac{1}{2}}}} exp(-\frac{1}{2}(x – \mu)^T \Sigma^{-1}(x – \mu))\)
\(p(x) < \epsilon\)なら異常と判断

以下オリジナルのガウス分布と多変量ガウス分布の関係性についてです。

多変量ガウス分布に制約を加えた者がオリジナルのガウス分布となっています。
その制約とは共分散行列である\(\Sigma\)の非対角成分が0でなくてはならないということです。

多変量ガウス分布は共分散行列の非対角成分が0ではなかったので、そういうことですね。
ただ、元をたどればオリジナルも多変量ガウス分布も計算する式の理論は同じだそうで。

以下オリジナルのガウス分布と多変量ガウス分布の使い分けについてです。

オリジナルのモデル
・頻繁に使われる
・異常な組み合わせの値となるアノマリーを検知したいとすると、\(x_1\)と\(x_2\)の組み合わせた\(x_3\)を作成する必要がある。
・計算コストが小さい(特徴数が多くても大丈夫)
・トレーニングセットが相対的に小さくても割と機能する

多変量ガウス分布
・使用量は少し
・特徴間の相関を捉えることができる
・計算コストが高い(特徴量が多いと危うい)
・アルゴリズムにある種の性質があるため、\(m>n\)つまり手本の数は特徴の数より大きくしなければいけない。\(m<n\)になってしまうと、共分散行列が可逆ではなくなり特異行列となってしまい、何かしら変更しないと多変量ガウス分布のモデルは使うことができなくなる。先生は\(m>10n\)くらい差がないと使わないみたいです。多変量ガウス分布は共分散行列として\(n×n\)のパラメータを使用するため、それに見合うだけの\(m\)数がないといけないということですね。
・上記補足：共分散行列が特異行列になってしまう原因は2つあり、1つは\(m>n\)を満たしていないこと、2つ目は冗長な特徴があることです。ここでいう冗長な特徴とは、特徴が重複していることで\(x_1=x_2\)となっていたり\(x_3=x_4+x_5\)と既存の特徴を使用しただけで新たな特徴ではないものが含まれていることが原因となりシグマは非可逆となってしまう。

Recommender Systems

Problem Formulation

レコメンダシステム(Recommender System)についての説明です。
機械学習の応用として、レコメンダシステムが使われることが多いです。
今まで特徴を手動で選んだり調整していましたが、レコメンダシステムでは自動で選択してくれます(以前話していたものですね)。

レコメンダシステム（英: recommender system）は、情報フィルタリング (IF) 技法の一種で、特定ユーザーが興味を持つと思われる情報（映画、音楽、本、ニュース、画像、ウェブページなど）、すなわち「おすすめ」を提示するものである。通常のレコメンダシステムは、ユーザーのプロファイルを何らかのデータ収集基準と比較検討し、ユーザーが個々のアイテムにつけるであろう評価を予測する。基準は情報アイテム側から形成する場合（コンテンツベースの手法）とユーザーの社会環境から形成する場合（協調フィルタリングの手法）がある。(Wikipediaより引用)

今回は例として映画の評価の予測を行います。
ある年の映画を見て、数人のユーザーが評価をつけました。以下がその図です。

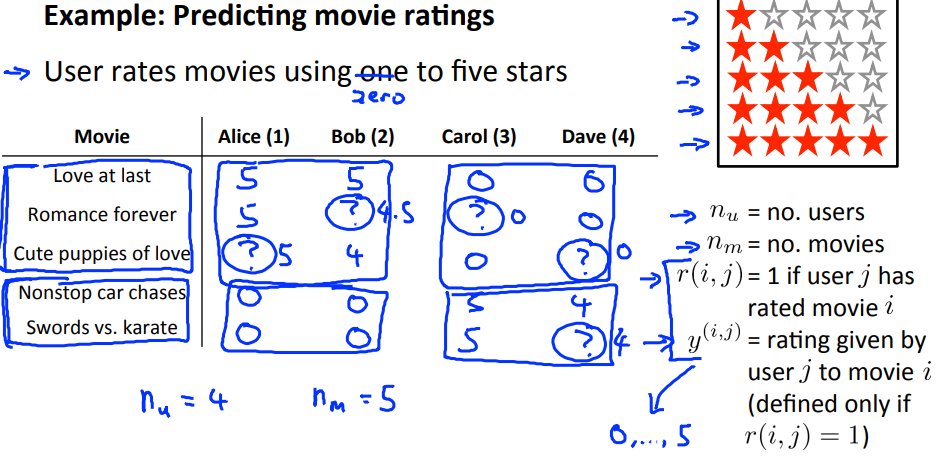
上記の画像の右側にある表記の説明は以下になります。

表記	意味	例での値
\(n_u\)	ユーザー数	4
\(n_m\)	評価対象映画数	5
\(r^{(i,j)}\)	ユーザー\(j\)が映画\(i\)を評価済みの場合1	\(r^{(3,1)}=0,r^{(2,4)}=1\)
\(y^{(i,j)}\)	ユーザー\(j\)の映画\(i\)の評価	\(y^{(5,3)}=5,y^{(3,4)}=undefined\)

Content Based Recommendations

レコメンダシステムを作成するにあたり、最初のアプローチについて説明しています。
言い換えると、コンテントベースのレコメンデーション(Content Based Recommendations)についてとなります。

前回の映画を例として使用すると、映画に特徴\(x_1,x_2\)を追加します(ベクトルで表現可能)。
また、その特徴量\(x^{(i)}\)を映画の上から順番に\(x^{(1)},x^{(2)}\)として、ユーザーも同じように順番毎に学習するべきパラメータを設定します\(\theta^{(1)},\theta^{(2)}\)(設定方法は後程)。(切片項として\(x_0=1\))

これらを使用し、ユーザーの評価を予測すると下記の式で算出できます。

\(y^{(i,j)} = (\theta^{(j)})^{T} x^{(i)}\)

以下参考図です。

では、パラメータ\(\theta\)を求めるにはどうすれば良いか？

以下が最適化の目的関数です。正則化項も入っています。

上記の図での上の式は求めるパラメータは一人用であり、下の式が全員分計算できるようになっている(\(\Sigma\)が一つ追加されている)。

その後、最急降下法を使用して、パラメータを最適化します。

本質的には線形回帰と同じですね。

Collaborative Filtering

協調フィルタリングについての内容です。
別名フィーチャーラーニングと呼ばれています。これはアルゴリズム自身が何の特徴を使用するかを自分自身で学習するということです。

前回使用した映画の特徴ですが、それぞれの特徴を各ユーザーから聞くのだとコストが高いです。
そこで、前回とは逆にパラメータ\(\theta\)を使用して特徴である\(x^{(i)}\)を予測します。

これで前回の講義と合わせて、特徴が分かればパラメータを推測できる。パラメータが分かっていれば特徴を推測できるようになりました。

上記を踏まえた上で、最初に行うことは、ランダムにパラメータ\(\theta\)の値を推測することです。それを用いて\(x\)を推測し、その\(x\)から\(\theta\)を推測するという繰り返しを行います。繰り返していくうちに\(x\)と\(\theta\)の値が改善されていきます。

この協調フィルタリングの弱点として、これが可能なのは各ユーザーが複数の映画を評価していて、全ての映画が複数のユーザーに評価されて初めて可能となる点です。

Collaborative Filtering Algorithm

協調フィルタリングのアルゴリズムについてです。
前回は\(x\)と\(\theta\)を行ったり来たりで繰り返し計算していましたが、効率が悪いので同時に計算してみます。

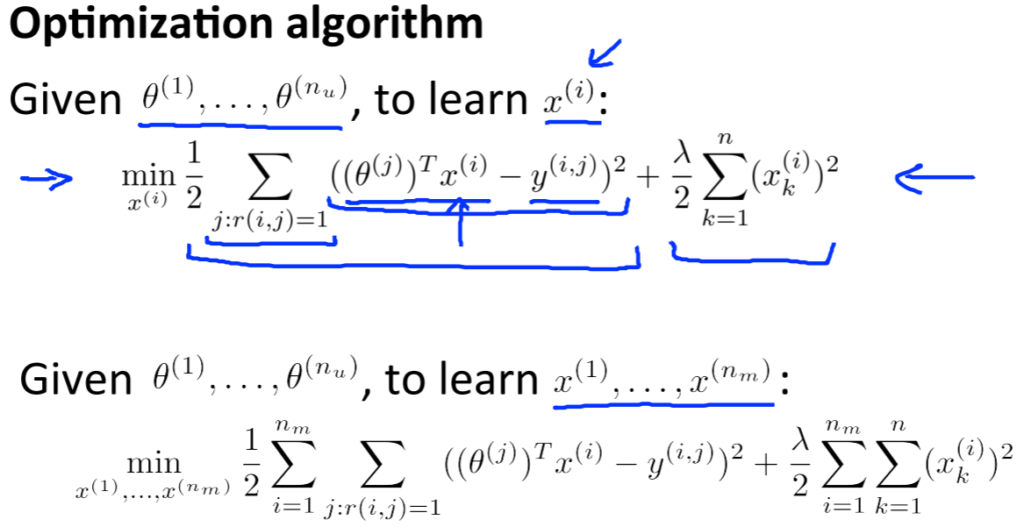
ここで一度\(x\)と\(\theta\)を求める式の説明をします。

二つの式はとても似ています。上の式では、最初の\(\Sigma\)で各ユーザー\(j\)をとり、次の和でそのユーザーによって評価された全ての映画について和をとっています。その下の式は逆のことを計算しているだけですね。

一番下にある式が合わせた関数になります。ちなみに、複合させた関数で\(x\)または\(\theta\)を定数とすると、上で表した\(x\)のみ\(\theta\)のみの計算ができます。
また、以前は切片項\(x_0=1\)を含んでいたため、\(x\in \mathbb{R}^{n+1}\)だったが、今回は特徴も学習するため、切片項はなく\(x\in \mathbb{R}^{n}\)となります。パラメータ\(\theta\)も同じ理由であり同じ次元なので、\(\theta\in \mathbb{R}^{n}\)となります。いつもアルゴリズムが1となる特徴を必要としているなら、学習結果でおのずと1となるのも理由です。

今回のまとめです。
協調フィルタリングのアルゴリズムのステップです。

1.まず、パラメータ\(x^{(1)}, …, x^{(n_m)}, \theta^{(1)}, …, \theta^{(n_u)}\)をある小さなランダムな値で初期化します(Symmetry Breaking)。
Coursera Machine Learning / week5【学習メモ】

2.目的関数である、\(J(x^{(1)}, …, x^{(n_m)}, \theta^{(1)}, …, \theta^{(n_u)})\)の最小値を満たすパラメータを同時に学習します。

\({{J = \frac{1}{2} \sum_{(i,j):r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}}x^{(i)} – y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_m}_{i=1} \sum^{n}_{k=1}(x_k^{(i)})^2
+ \frac{\lambda}{2}\sum^{n_u}_{i=1} \sum^{n}_{k=1}(\theta_k^{(j)})^2}
}\)

その後最急降下法などにより、パラメータを更新します。上の()の中の式は目的関数を特徴\(x^{(i)}\)で偏微分したものです。下の()の中の式は目的関数を特徴\(\theta^{(i)}\)で偏微分したものです。

\(x_k^{(i)} := x_k^{(i)} – \alpha (\sum_{j:r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}} x^{(i)} – y^{(i,j)})\theta^{(j)}_k + \lambda x^{(i)}_k)\)

\(\theta_k^{(i)} := \theta_k^{(j)} – \alpha (\sum_{i:r(i,j)=1} ((\theta^{(j)})^{\mathrm{T}} x^{(i)} – y^{(i,j)})x^{(i)}_k + \lambda \theta^{(j)}_k)\)

3.学習したパラメータを使用して、各ユーザーの評価を予測します。

\(y^{(i,j)} = (\theta^{(j)})^{T} x^{(i)}\)

Vectorization: Low Rank Matrix Factorization

協調フィルタリングのベクトル化した実装です。別名低ランク行列分解と呼びます。
また、協調フィルタリングとして、アマゾンなどで関連のある標品をおすすめしてくることがありますが、その方法について説明されています。

以下は映画の評価表と評価表を\(Y\)という行列に入れています。

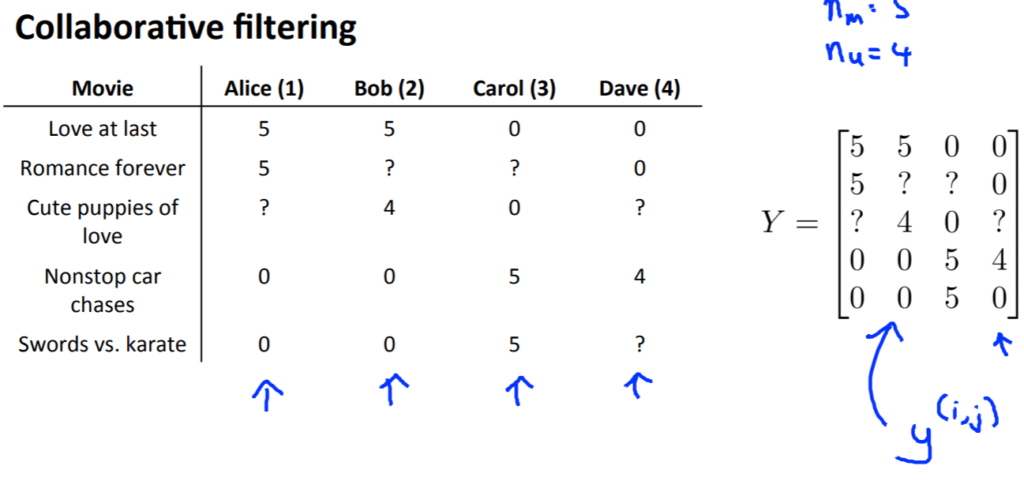
\(Y\)という行列は、一つ一つが\(y^{(i,j)} = (\theta^{(j)})^{T} x^{(i)}\)という式で求めることができます。
つまり、下記の図のように表すことができます。

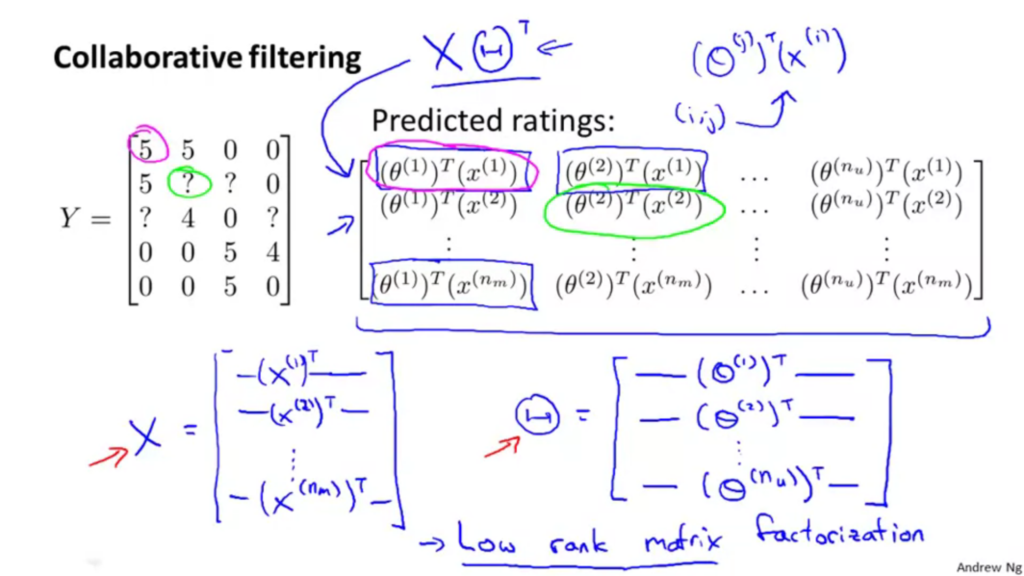
もっと簡単にするために、

\(X = \begin{bmatrix} – & (x^{(1)})^T & – \\ & \vdots & \\ – & (x^{(n_m)} & – \end{bmatrix}\)
\(\Theta = \begin{bmatrix} – & (\theta^{(1)})^T & – \\ & \vdots & \\ – & (\theta^{(n_u)} & – \end{bmatrix}\)
\(Y = X\Theta^T\)

と転置を使用してコンパクトにしています。こうするとランク(次元)が低くなるので低ランク行列分解と呼ばれています。

では、映画を見たときに関連する映画をオススメする方法とは。
映画の特徴量を\(x^{(i)} \in \mathbb{R}^n\)と表すと、学習した特徴を利用して二つの映画がどれくらい近いのかをこの式\(||x^{(i)}-x^{(j)}||\)で計算し、結果が小さい(距離が近い)と類似性があるということになります。

Implementational Detail: Mean Normalization

平均標準化(mean Normalization)を使って実装を改善することについて説明しています。

とあるユーザーが映画の評価を一つもしていない場合、前回出てきた式を使って各映画に対する評価を予測しようとすると全て0になってしまいます。

それを防ぐために、平均標準化を使用します。

以下がまとめ図です。

1.以前同様全ての映画の評価を\(Y\)の行列にグルーピングします。

2.各映画の得た評価の平均を計算し(このとき未評価の数は含まない)、\(\mu\)というベクトルに保存します。

3.\(Y\)の各値から\(\mu\)を引き、平均標準化したデータセット(平均が0)を作成します。

4.3で作成した平均標準化したデータセットを使用して、パラメータ\(x\)と\(\theta\)を学習させます。

5.4で算出したパラメータ\(x\)と\(\theta\)を利用して、ユーザの評価を予測します。

\((\theta^{(j)})^{T}(x^{(i)})+\mu_i\)

ここでは平均標準化したデータセットを作成する時に平均を引いて算出したため、一度平均\(\mu\)を足して戻す必要があります。

結果、今回の全ての映画が未評価のユーザーの場合は平均値が評価として扱われることになります。

平均標準化についてはweek2で学習したものと似ています。違う点としては最大値-最小値という計算ができない点です。これは、今回の映画の評価を例に説明すると、既に比較可能となっているため同様のスケールになっているからです。

さいごに

前回の投稿から大分期間が空いてしまいましたが、無事week9終了しました。
内容量は全weekの中で一番長かったと思います(一番難しかったのはニューラルネットワーク)。ブログもその分長いです。
今回は異常検知とレコメンダシステムを学習しました。教師なし学習と教師あり学習との関係性についても明らかになりました。尚、プログラミング課題はweek9までみたいで、week10とweek11は内容量はとても少ないみたいです。一山超えた気持ちです(笑)。

振り返ると、ブログに数式を記載するのも全く苦にならなくなりました。指が勝手に動いてくれます。また、講義はすべて英語ですが、何となく何を言っているのかわかる部分が増えました。一カ月以上ほぼ毎日リスニングしているようなものだからですかね。相変わらず先生の講義は分かりやすくてスッと頭に入ってきます。

残すところ、week10とweek11のみですが、引き続き頑張っていきます！